A Ciência de Dados é uma das áreas com maior crescimento na atualidade, e o fator determinante para seu crescimento é o grande volume de dados, nunca visto antes. Em outras palavras, um fluxo constante e exaustivo de dados é produzido na atualidade, sendo que ao se agregar valor se tornam informações valiosas para tomada de decisões.

A intercessão entre três áreas de conhecimento: matemática e estatística, ciência da computação e conhecimento das áreas de negócio, compõe os três pilares para a área de ciência de dados.

Neste artigo, vamos falar de estatística. Este é um pilar mais teórico e muitas vezes pode ser temido por sua complexidade. Mas o grande segredo para obter uma análise de dados mais fluida está em entender os principais conceitos dessa área.

O que é estatística?

Estatística é a ciência, parte da matemática aplicada, que fornece métodos para coletar, descrever, analisar, apresentar e interpretar dados para a tomada de decisões.

Ciência de dados e estatística não devem ser confundidas, uma vez que os propósitos são por muitas vezes os mesmos, mas as formas de estudo não são. A teoria estatística serve de base para ciência de dados. A ciência de dados utiliza a estatística para buscar padrões em meio a incertezas.

A American Statistical Association (ASA) reconheceu que “a ciência de dados abrange mais do que estatística, mas a estatística desempenha um papel fundamental no rápido crescimento desse campo”.

A estatística está dividida em três áreas: estatística descritiva, estatística inferencial e probabilidade. Vamos discutir nesse artigo um pouco sobre estatística descritiva.

Fundamentos de descrição de dados

Durante o processo de análise de dados, a etapa inicial consiste em descrever e resumir os dados para apresentação. Etapa essa que é embasada teoricamente pela estatística descritiva.

Formalmente, estatística descritiva é a fase em que são utilizados métodos para coleta, organização, apresentação, análise e síntese dos dados.

Os conceitos de estatística de descritiva estão mais presentes em nosso dia-a-dia do que a gente pode imaginar. Você já ouviu falar de média ou mediana? Até mesmo de desvio padrão e variância? Esses nomes referem-se a resumos dos dados, alguns de centralidade e outros de dispersão de uma determinada variável.

Variável é a característica de interesse que é medida em um determinado conjunto de dados. Por exemplo, podemos estar interessados em analisar a situação epidemiológica do Brasil devido à pandemia do Covid-19. Então, algumas variáveis de interesse são: número de infectados pelos Covid-19, número de mortes causadas pelo Covid-19, etc.

Ao estudarmos as medidas de tendência central ou de dispersão dessas variáveis, estamos estudando essas variáveis de uma forma individual.

Mas, podemos estar interessados em entender como algumas variáveis se comportam em conjunto. Por exemplo, ao invés de entender o número médio de infectados pelo Covid-19 no Brasil, podemos estar interessados em entender qual a relação do número de infectados com o número de mortos pelo Covid-19.

Nesse caso teremos duas variáveis e precisamos avaliar o seu relacionamento. Para descrevê-la estatisticamente, usamos o coeficiente de correlação.

O que é coeficiente de correlação?

O coeficiente correlação mede o grau de relação entre duas variáveis, isto é, o quanto a alteração de valores em uma variável provoca alteração de valores de outra variável. Por exemplo, o quanto a alteração do número de infectados pelo Covid-19 modifica o número de mortes causadas pelo Covid-19.

Como calcular o coeficiente de correlação?

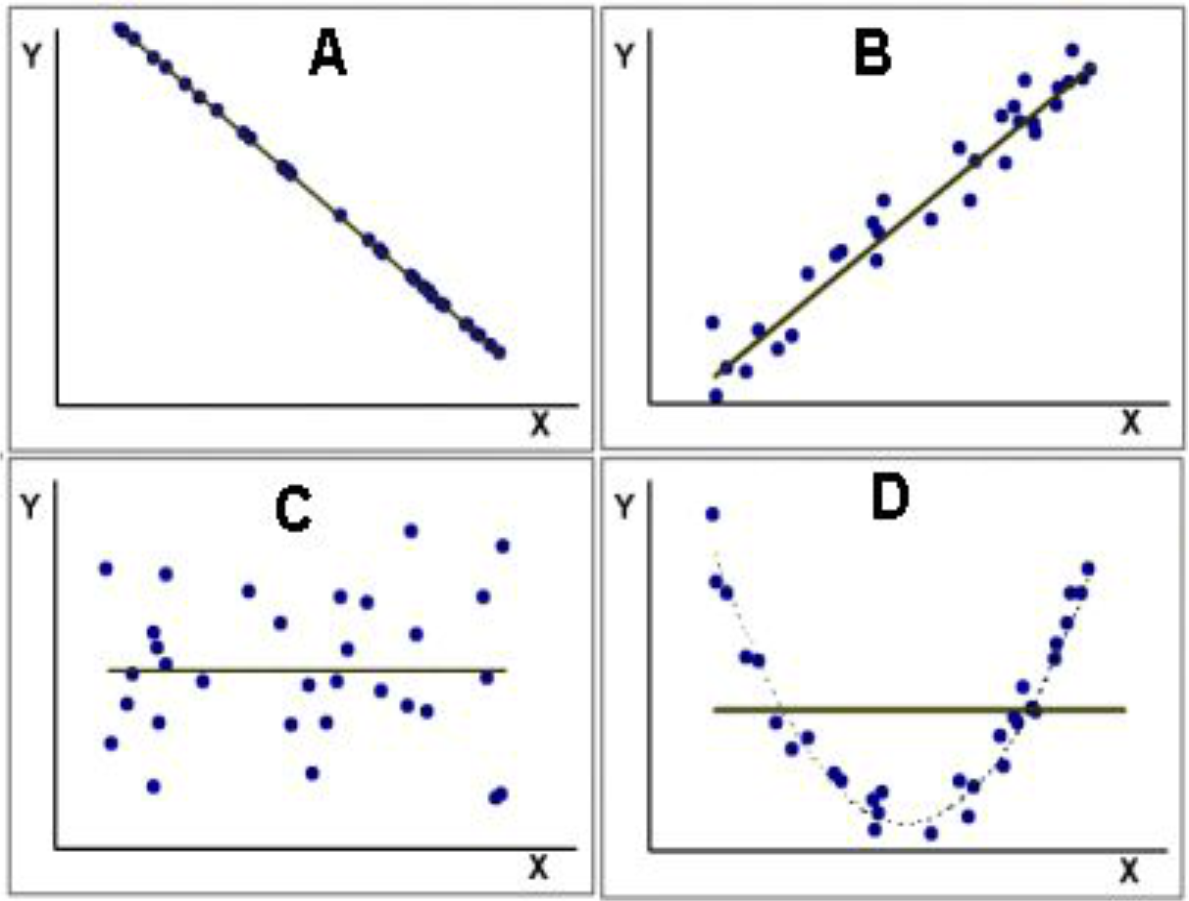
Existem algumas formas de se calcular o coeficiente de correlação que são aplicadas de acordo com a forma como as variáveis se comportam. Em geral, para entender a forma como essas variáveis se comportam, um diagrama de dispersão é plotado. Suponha que X = número de infectados pelo Covid-19, e Y = número de mortos pelo Covid-19. Veja a imagem abaixo:

Fonte: http://medstatweb.med.up.pt/cursop/print_script1f0d.html?capitulo=regressao&numero=3&titulo=Correla%E7%E3o%20e%20regress%E3o%20linear%20simples

A Figura 1 é composta por quatro cenários possíveis de correlação:

A – Há uma relação linear perfeita entre X e Y, porém negativa, ou seja, quando o X aumenta, Y diminui

B – Há uma relação linear forte entre X e Y, porém positiva, ou seja, quando X aumenta, Y também aumenta

C – Não existe relação linear entre as variáveis X e Y

D – Existe uma relação NÃO linear entre as variáveis X e Y

A análise gráfica é importante para entender a forma, mas não fornece uma dimensão do grau de correlação. Existem alguns coeficientes de correlação mais populares, que mostraremos a seguir.

Coeficiente de correlação de Pearson

O coeficiente de correlação de Pearson, também denotado por r, é dado por uma função da covariância entre X e Y, ou seja, da medida de variabilidade conjunta entre X e Y. Ele é utilizado para medir relações lineares.

O coeficiente r será um número que varia entre -1 e 1, valor que nos diz o grau de intensidade da relação entre as variáveis da seguinte forma:

• Quanto mais próximo de -1: maior correlação linear negativa
• Quanto mais próximo de 1: maior correlação linear positiva
• Quanto mais próximo de 0: menor a correlação linear

Coeficiente de correlação de Spearman

O coeficiente de correlação de Spearman é utilizado para dados não lineares e também provê um coeficiente que varia entre -1 e 1, cuja interpretação do coeficiente de Pearson se estende.

Se o cálculo é feito através de postos, os dados são ordenados de uma forma crescente e cada elemento dos dados recebe um posto.

Esse coeficiente é ideal quando as variáveis possibilitam esse tipo de ordenação, isto é, são ditas variáveis ordinais e nenhuma suposição de linearidade é feita.

Coeficiente de correlação de Kendall

O coeficiente de correlação de Kendall é uma extensão do coeficiente de correlação de Spearman, pois também o método de classificação em postos da variáveis.

Porém, o coeficiente de Kendall é mais preciso, portanto é indicado para situações em que estamos lidando com amostras pequenas.

Apesar de medir o valor da relação entre duas variáveis, devemos sempre ter em mente que correlação é DIFERENTE de causalidade. Suponha que haja uma correlação linear positiva forte entre X e Y através do coeficiente de correlação de Pearson. Isso não quer dizer que a causa do número de mortes ser maior é o número de infectados estar maior, mas apenas que existe uma relação positiva entre essas variáveis.

Estudo de Caso

Analisamos os dados do Covid-19 até o dia 05 de junho de 2020 interessados em entender se o número de infectados e o número de mortos forneceriam algum tipo de correlação.

 

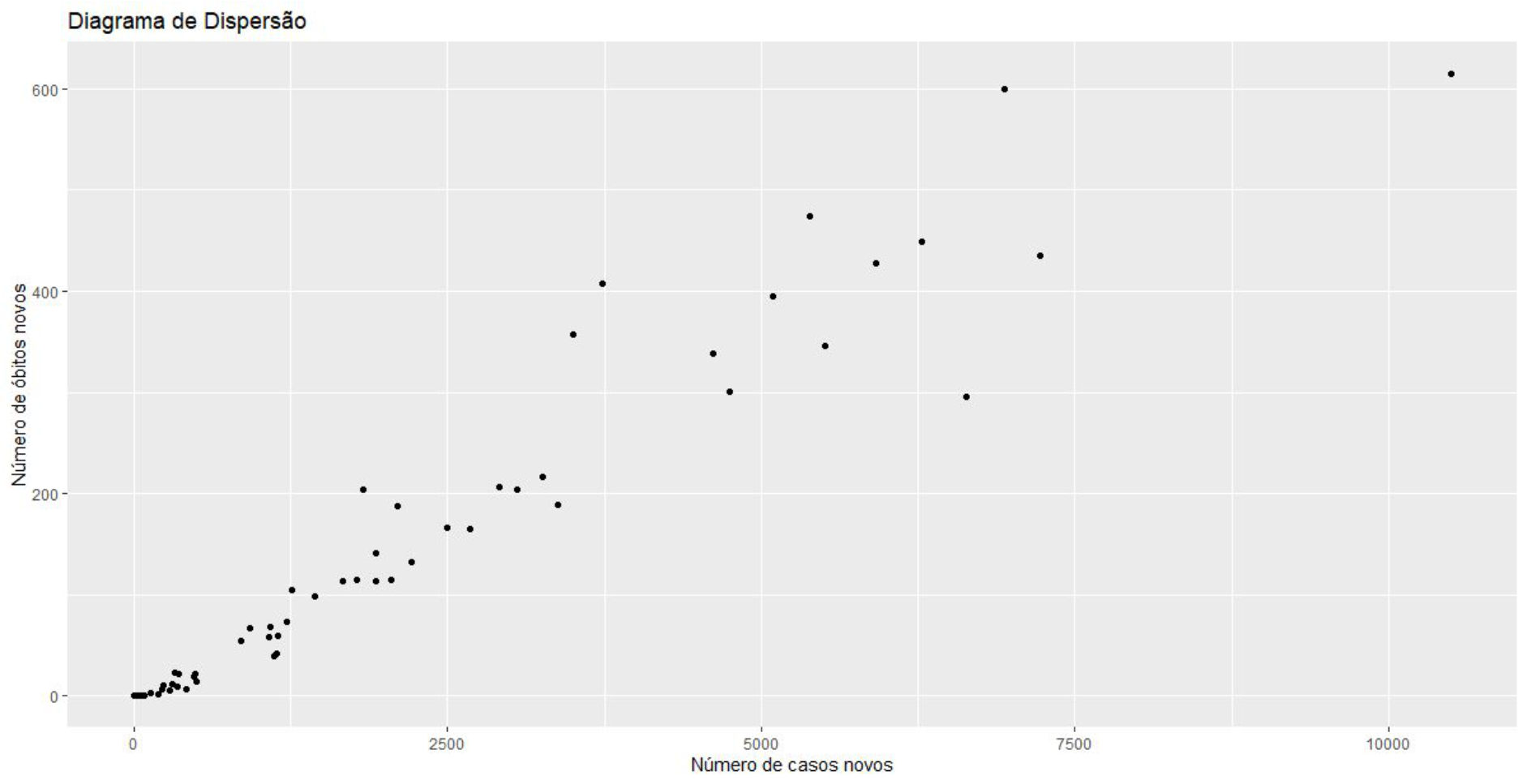
Diagrama de dispersão para os dados do Covid

Graficamente, observamos o indício de uma correlação linear forte entre o número de novos casos e o número de novos óbitos pelo Covid-19. De fato, esse comportamento é esperado pelo senso comum da população. Mas só podemos afirmar que essa correlação existe ao calcularmos o seu valor.

Como observamos que essa relação se comporta de forma linear, o coeficiente de correlação de Pearson foi calculado e igual a 0,96. Esse valor encontrado corrobora a nossa suspeita inicial de que há uma relação linear forte entre as duas variáveis.

Ainda, o valor dessa correlação pode ser testado estatisticamente, através de testes de hipóteses. Mas, isso é tema para um próximo artigo, não deixe de acompanhar!

O uso de análise de correlações não se restringe ao nosso estudo de caso, e pode ajudar a nortear diversos estudos. Podemos estar interessados em acompanhar peso e altura de crianças para se estabelecer uma curva de crescimento, número de acidentes de trânsito com índice de pluviométrico para decisão de medidas preventivas, entre outros.

Portanto, o valor da correlação pode contribuir não somente para a análise estatística, como também para a população em geral, pois fornece de forma confiável informações valiosas que, mesmo que não impliquem em causalidade, auxiliam na resolução de problemas e em tomadas de decisão. Esses dois impactos, frequentemente sobrepostos, são essenciais para o bem estar da população.

 

Autor(a): Jéssica Assunção, MSc – Estatística na DataSprints

Revisores(as):

Luis Martins – CEO na DataSprints

Danilo Costa – Cientista de Dados Líder na DataSprints

Rodrigo Araújo, PhD – Redator Técnico e Cientista de Dados na DataSprints