INTRODUÇÃO
Assim como as ciências básicas (matemática, biologia, química, física, dentre outras), que nos permitem descrever detalhadamente a natureza, a análise de dados desempenha um papel fundamental na produção de novos conhecimentos e na descrição de alguns fenômenos. E com o avanço da tecnologia e do conhecimento, foi possível aplicar as ciências básicas na análise de dados e começar a explicar, modelar e prever o curso da disseminação de doenças.
A pandemia do Covid-19 já infectou mais de 13 milhões de pessoas ao redor do mundo, tendo milhares de casos mortais. Em outros períodos da humanidade, já aconteceram eventos semelhantes:
- A peste bubônica matou entre 75 e 200 milhões pessoas na Europa durante o século 14. Estima-se que a praga pode ter sido responsável por reduzir a população mundial de 450 milhões de pessoas para 350 milhões, uma redução de quase 25%.
- A varíola teve uma estadia prolongada, cerca de 3 mil anos. Relatos históricos mostram que o faraó egípcio Ramsés II, a rainha Maria II da Inglaterra e o rei Luís XV da França foram contaminados. Em 1980 teve sua erradicação devido à vacinação em massa.
- A cólera teve sua primeira aparição em 1817, matando centenas de milhares de pessoas. Desde então, vem apresentando ciclos epidêmicos esporádicos, e, portanto, ainda é considerada uma pandemia. Em 2019, o Iêmen teve mais de 40 mil mortes por cólera.
- A gripe espanhola surgiu em 1918 e estima-se que entre 40 e 50 milhões de pessoas tenham morrido devido a ela ao redor do planeta, tendo infectado mais de um quarto da população mundial. É uma doença oriunda da Europa, tendo chegado ao Brasil a bordo do navio Demerara, um transatlântico que desembarcou passageiros infectados no Recife, em Salvador e no Rio de Janeiro.
- O H1N1 foi a primeira pandemia do século 21, no ano de 2009. Matou cerca de 16 mil pessoas pelo mundo. No Brasil, o primeiro caso foi confirmado em maio, e no fim de junho eram 627 pessoas infectadas no país, de acordo com o Ministério da Saúde.
Considerando os séculos em que as outras pandemias ocorreram, em nenhuma delas tínhamos tecnologia, desenvolvimento e entendimento suficientes para analisar o cenário como um grande banco de dados. Mesmo o H1N1, ainda nesse século, não teve tanta repercussão quanto a pandemia atual do Sars-Cov-19. No entanto, o estudo analítico dessas doenças e de outras tornou possível desenvolver uma modelagem matemática que descreve a propagação dessas doenças infecciosas. O primeiro registro de um estudo de modelagem é datado de 1760, com o trabalho de Daniel Bernoulli sobre a varíola. Em 1906, William Hamer foi o primeiro a prenunciar o princípio da Lei de Ação das Massas [1]. Ele teve como objetivo analisar e modelar o comportamento e a evolução de uma doença em uma determinada população do tempo. Isso mostrou que com um modelo é possível auxiliar no controle da propagação da doença, de modo a evitar o avanço de epidemias. Prever ações de vacinação e suas consequências, em suma, para ajudar na tomada de decisões.
Porém, com o desenvolvimento tecnológico, estes modelos clássicos, que consideram a taxa de transmissão fixa, produzem apenas previsões simplificadas, já que não consideram a mudança comportamental da população [2]. Uma vez que o comportamento dos indivíduos pode alterar de modo drástico o curso da disseminação de uma epidemia, faz-se necessário compreender os fenômenos sociais ligados às diversas culturas. Com isso é possível aprofundar o conhecimento de como uma doença se espalha na população, como sua transmissão e as medidas de prevenção [3]. Em outras palavras, o modelo considera a resposta da população sobre a doença, deste modo as medidas preventivas podem ser alteradas conforme os novos dados.
Desde o início da pandemia, a mudança de hábitos, como o uso de máscara e a adoção de hábitos de higiene mais rigorosos, assim como as medidas não farmacológicas adotadas no combate ao Sars-cov-19 como a quarentena, distanciamento social, isolamento e lockdown, fazem parte do conjunto de elementos associados ao comportamento da população. No Brasil, estudos já concluíram que tais medidas são benéficas e seus efeitos positivos podem ser percebidos em até 14 dias após sua aplicação [4].
Podemos pensar ainda nas variáveis que os dados clínicos podem apresentar ao considerarmos qualidade e consistência, por exemplo, casos de pacientes falso-positivos. O emprego de Big Data (ou seja, o processamento um grande volume de dados para obter conclusões) pode auxiliar na verificação de conformidade dos dados, na correlação com os dados comportamentais, que podem ser computados e analisados com facilidade, a fim de sofisticarmos o mapeamento da propagação do vírus. Exemplos de análises que podem ser feitas a partir de Big Data:
- Análise descritiva: utiliza-se de metodologias e tecnologias para descrever a situação atual e passada dos fenômenos, cujos dados são representados de maneira sintética e gráfica;
- Análise preditiva: ocorre por meio de análises estatísticas de dados que ajudam a entender o que pode acontecer no futuro;
- Análise prescritiva: baseada nos dados da análise preditiva, pode-se identificar soluções estratégicas e operacionais eficazes, como a quarentena e sua flexibilização;
- Análise automatizada: as ações da análise preditiva são implementadas de forma automatizada e de acordo com o resultado das análises que foram realizadas.
Portanto, a evolução da modelagem matemática epidemiológica utiliza as análises de Big Data para aprimorar os modelos matemáticos clássicos baseados em diferenciais compartimentados, uma vez que o maior desafio desses modelos é precisamente estimar os parâmetros epidemiológicos relacionados ao comportamento social. Se essa etapa não for a mais importante da modelagem, ela é, sem dúvida, uma das mais relevantes, pois ínfimas variações nesses parâmetros representam um grande impacto nos resultados finais. Ressaltamos que, independente do método de estimação utilizado, um bom resultado só pode ser obtido se houver uma quantidade adequada de dados de qualidade acerca da população e do comportamento da doença nos indivíduos em particular e na população como um todo. Em outras palavras, o Big Data é uma maneira de garantir que essas condições sejam cumpridas e uma boa análise realizada.
Um novo modelo que pode ser utilizado para prever as características do Covid-19 é o Modelo de ondas de contágio, que prevê o nível de contágio da população nas diferentes fases da epidemia. Assim como outros, este modelo leva em conta diversas variáveis, como visto em detalhes na próxima seção.
Modelo de ondas de contágio (OC)
Sabemos que a quantidade de casos, incluindo os de morte, acumulados deve apenas aumentar, inicialmente de forma acelerada (conforme aumenta a quantidade de casos e de mortes diários) e depois de forma desacelerada (conforme as quantidades diárias diminuem, após o pico da pandemia). Isso nos leva a gráficos com as seguintes formas, todos produzidos para fins deste artigo:
Gráfico 1 – Casos diários de Covid-19
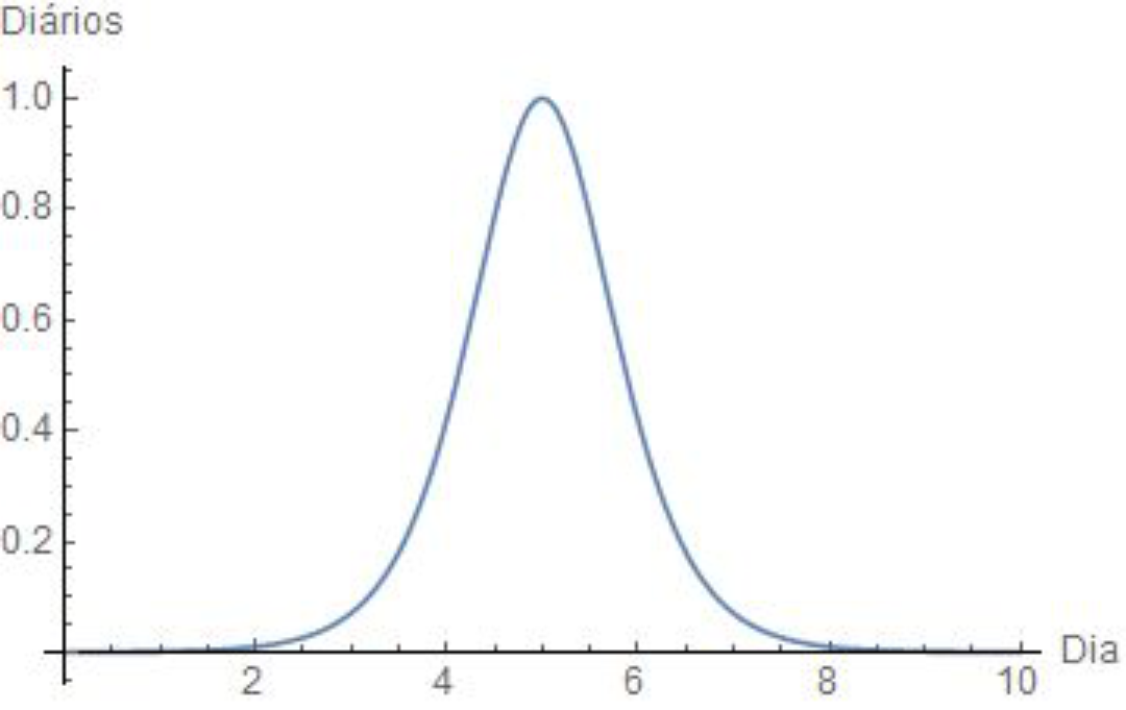
Gráfico 2 – Casos acumulados de Covid-19
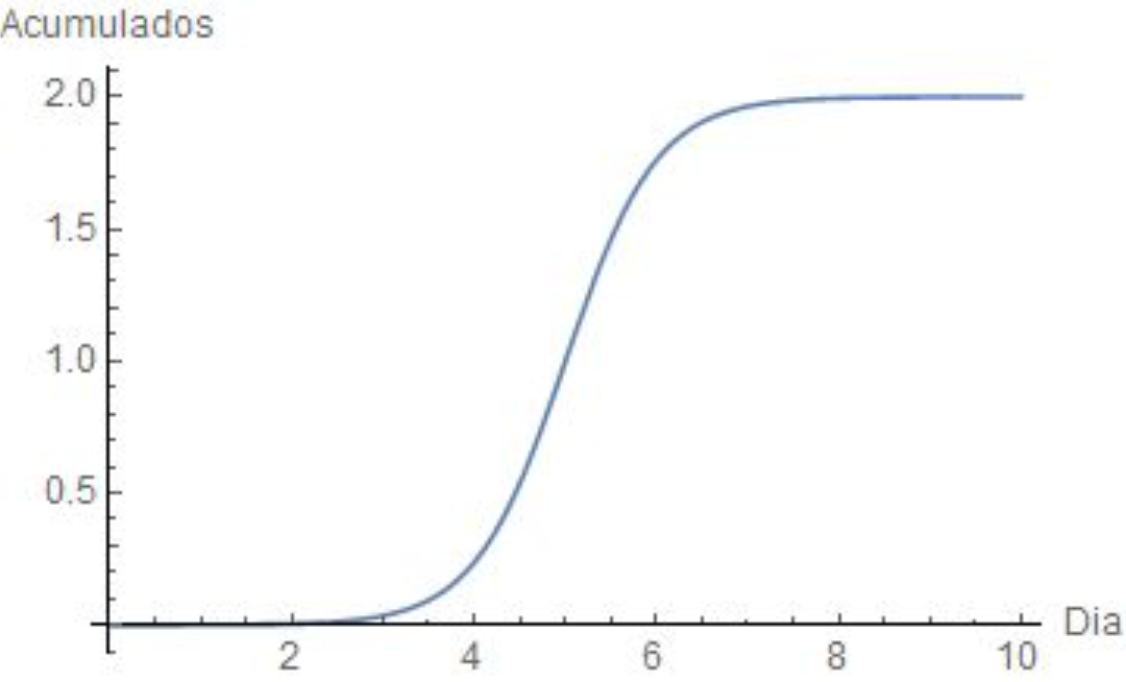
No Gráfico 1, para casos diários, temos um pico de casos por dia, o que seria o pico da pandemia. Já no Gráfico 2, temos o acumulado de casos, que corresponde à soma dos casos diários até a data indicada.
Sabendo das formas que estes gráficos devem ter, assumimos que os casos acumulados podem ser descritos por uma tangente hiperbólica (Gráfico 3), uma função matemática de forma semelhante ao do Gráfico 2, para os acumulados.
Gráfico 3 – Tangente hiperbólica
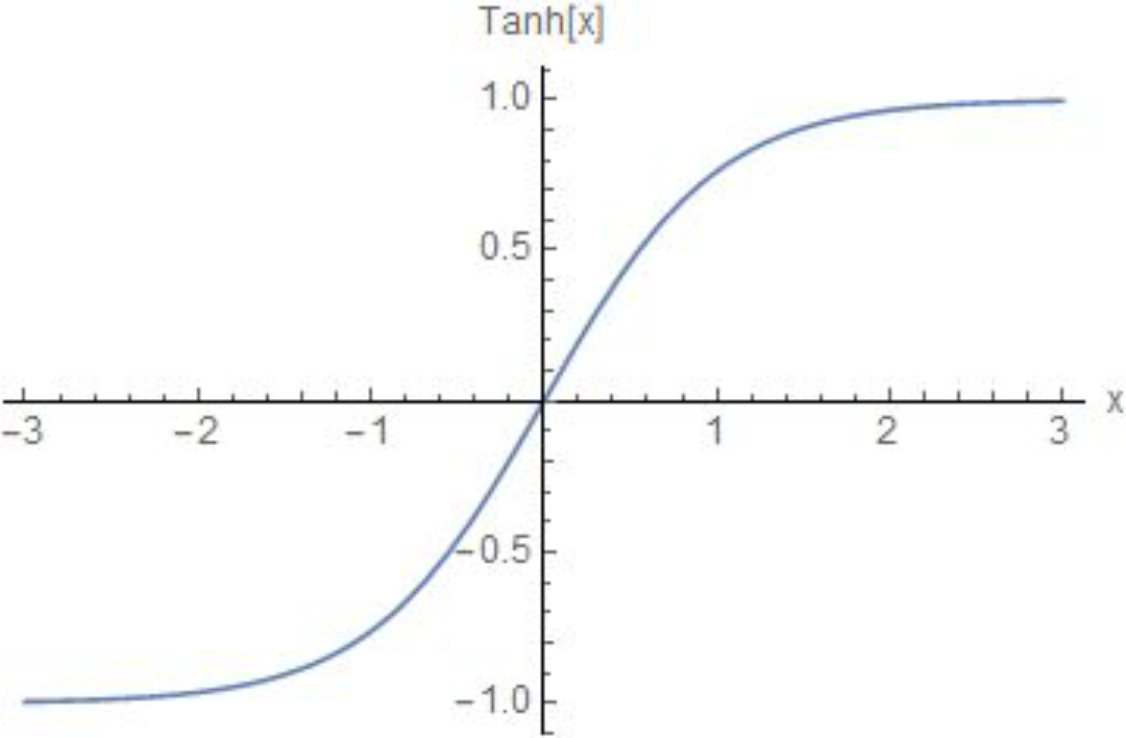
Contudo, a tangente hiperbólica, tal como no gráfico acima, não corresponde ao formato do gráfico de casos acumulados, dado que ela pode ter valores negativos e o ponto onde a função desacelera se encontra em x = 0. Para resolver este problema, consideramos o seguinte:
Acumulados = a Tanh(b x + c)+d
Acerca dos parâmetros a, b, c, e d, podemos obser:
- a, quando multiplicando Tanh(b x + c), permite que a função vá de -a até a, ao invés de -1 até 1, esticando a função para cima e para baixo. Isso é necessário pois não sabemos qual será o máximo de casos que a pandemia irá atingir, logo, precisamos ir além de 1.
- b, que multiplica x dentro de Tanh(b x + c), muda a inclinação da curva, permitindo que ela suba de maneira mais ou menos acelerada. Precisamos dele para ajustar a função tal que ela possa corresponder a velocidade com que os casos acumulados aumentam.
- c, que está sendo somado a bx no argumento da tangente hiperbólica, permite mover o gráfico como um todo para a esquerda e para a direita. Ajustando c podemos mover o gráfico de maneira que ele coincida com os dados de acordo com o dia.
- Por fim, quanto a d, é necessário para que não tenhamos uma quantidade negativa de casos. Lembremos que ao multiplicar por a fazemos o gráfico ir de -a até a, para eliminar a parte negativa somamos d, tal que o gráfico vá de d – a até d + a, onde d – a é positivo e corresponde a quantidade de casos no início da pandemia.
Uma vez que assumimos que os gráficos para os dados acumulados seguem a forma Acumulados = a Tanh(b x + c)+d, ajustamos os valores de a, b, c e d para que o gráfico da função coincida com o gráfico dos dados (em outras palavras, fazemos o ajuste da função para os dados). Nos gráficos abaixo, temos nossos melhores ajustes para os casos e mortes acumuladas no Brasil.
Gráfico 4 – Casos acumulados no Brasil
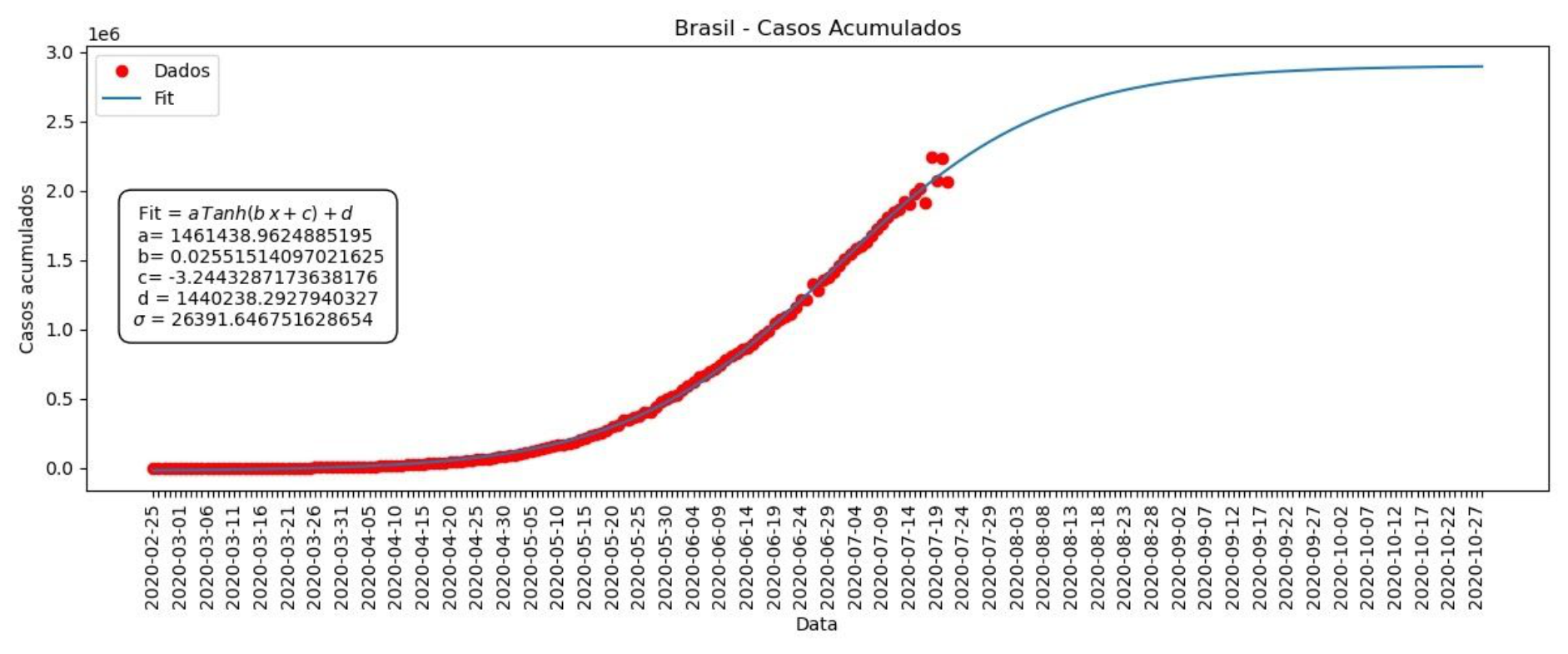
Gráfico 5 – Mortes acumuladas no Brasil
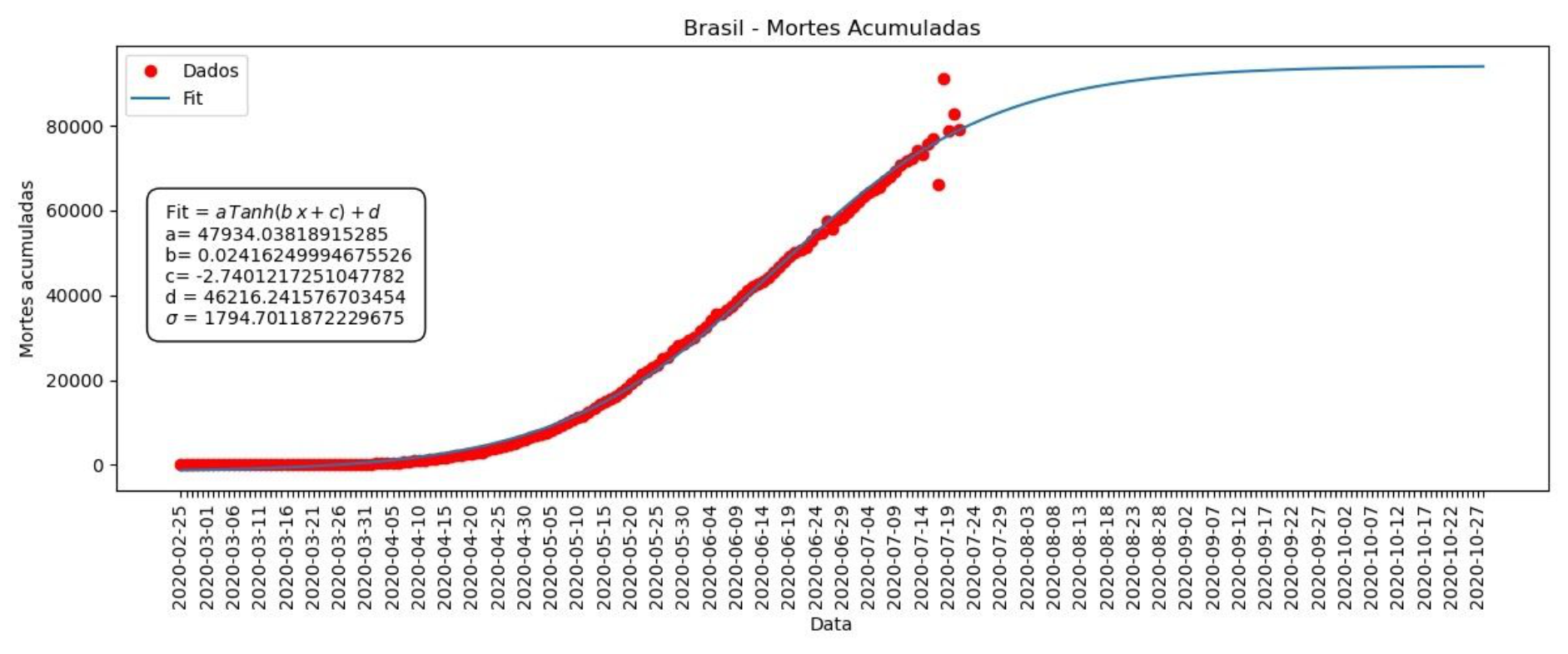
Nesses gráficos, temos os melhores valores encontrados para os parâmetros a, b, c e d. Também temos sigma (σ), que nos dá a precisão dos nossos ajustes. Sigma (σ) é uma média das diferenças entre nosso ajuste e os dados, quanto menor o sigma, melhor o ajuste. Podemos ver que os gráfico do ajuste do nosso modelo (Gráficos 4 e 5) segue de maneira bastante próxima à dos dados.
Para encontrarmos os gráficos para os casos e mortes por dia, tomamos a derivada da função para os Acumulados em relação ao tempo (dia). Derivadas nos dão a taxa de variação de uma função em relação a um parâmetro. Neste caso, a derivada de Acumulados em relação ao tempo nos dá o quanto os Acumulados aumentam a cada dia, o que corresponde à quantidade de casos/mortes por dia. A derivada da função dos acumulados tem a seguinte forma:
Diário = a b Sech2(b x + c)
Sech é a função secante hiperbólica. Desta maneira, derivamos as funções dos acumulados dos Gráficos 4 e 5 e fazemos os Gráficos 6 e 7 para os casos e mortes por dia apresentados abaixo.
Gráfico 6 – Casos por dia no Brasil
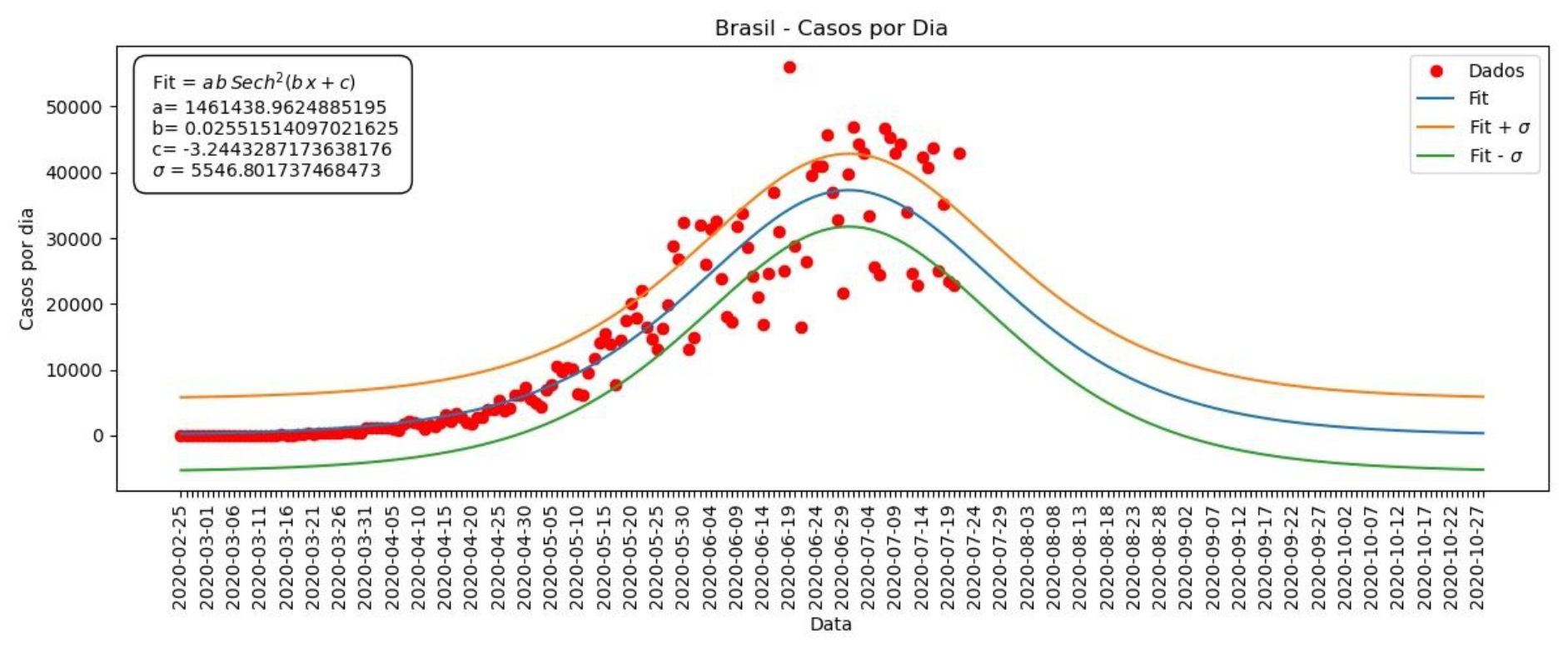
Gráfico 7 – Mortes por dia no Brasil
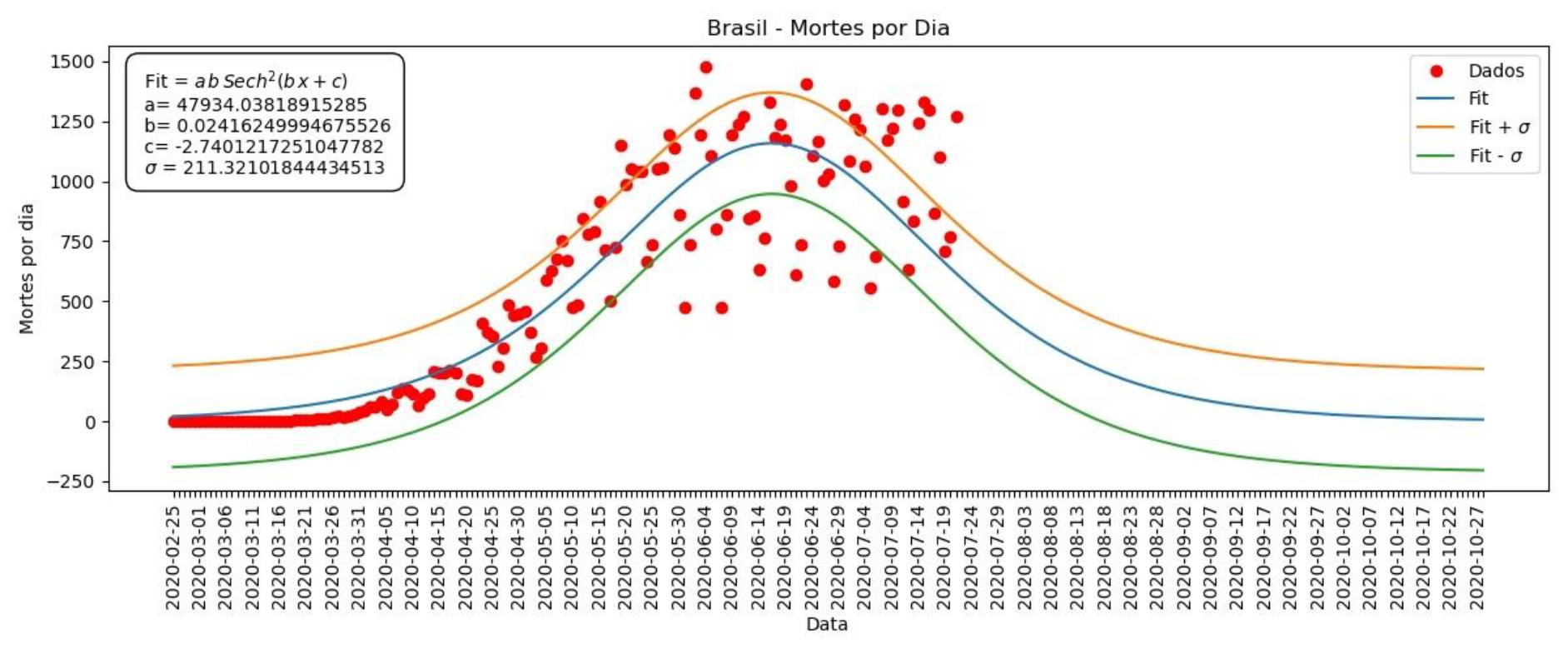
Desta vez, os gráficos dos nossos ajustes não seguem de maneira tão próxima os dados. Isso porque os casos/mortes por dia oscilam muito, mas ainda assim podemos ver que a maior parte dos dados se encontra no intervalo entre Fit+sigma e Fit-sigma. Desta forma, nosso ajuste nos permite dar uma estimativa dentro desta margem de erro, funcionando como uma média do que seria esperado. O mesmo vale para os casos/mortes acumulados.
Para os dados do Brasil nosso modelo (definido como Acumulados = a Tanh(b x + c)+d) teve sucesso, contudo, para o caso dos Estados Unidos temos uma situação diferente. No Gráfico 8, temos os casos por dia nos EUA.
Gráfico 8 – Casos por dia nos Estados Unidos
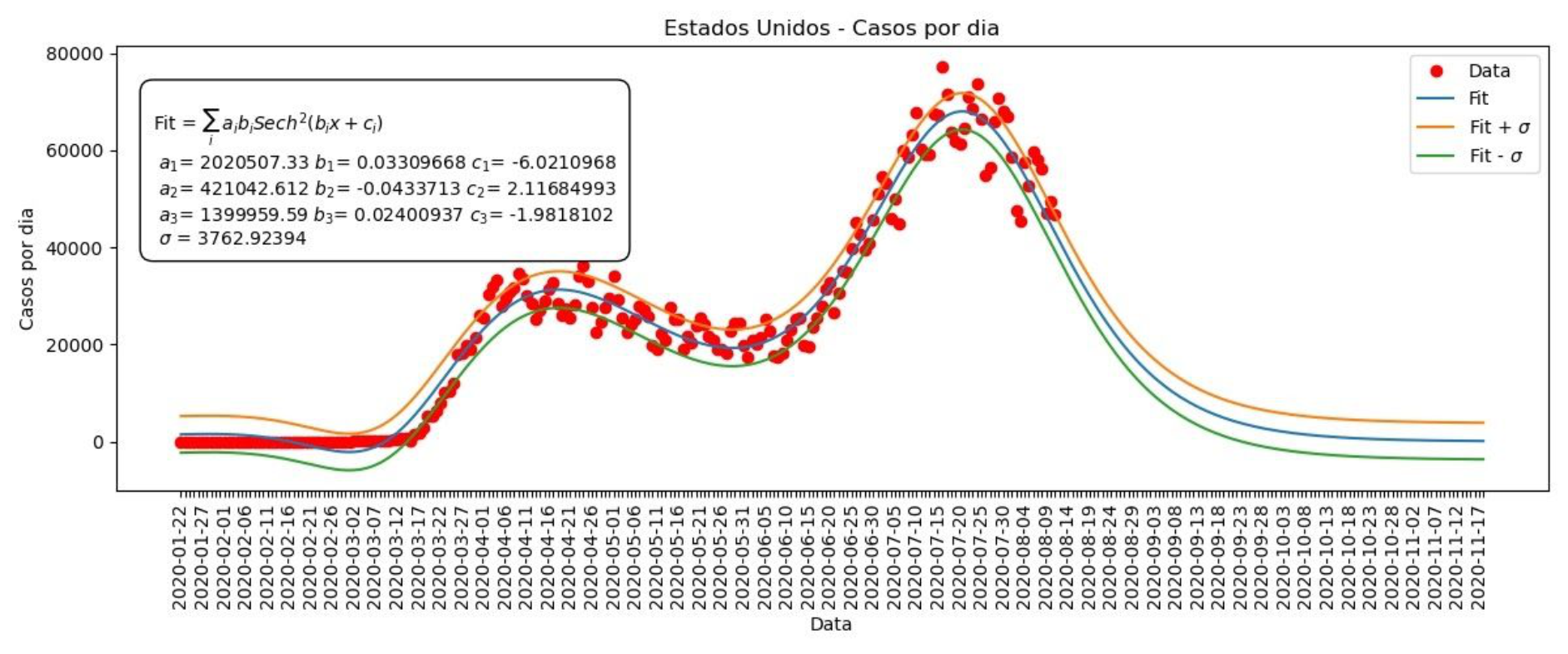
No caso do Brasil, temos apenas um pico nos casos diários, já para os EUA podemos identificar três picos, sendo que o último ainda não foi atingido. Neste caso, ao invés de considerarmos que a função para os casos acumulados tem apenas uma tangente hiperbólica, consideramos a soma de três tangentes na seguinte forma:
Acumulados = a1Tanh(b1x +c1) +a2Tanh(b2x +c2) +a3Tanh(b3x +c3) +d
Agora, como temos três tangentes hiperbólicas, temos três parâmetros a, b e c. Cada uma das tangentes representa uma onda de contágio, e os parâmetros distintos nos permitem ajustar cada uma das ondas de maneira que nosso modelo concorde com os dados. Para os casos acumulados e para mortes acumuladas e diárias temos os Gráficos 9, 10 e 11.
Gráfico 9 – Casos acumulados para os Estados Unidos
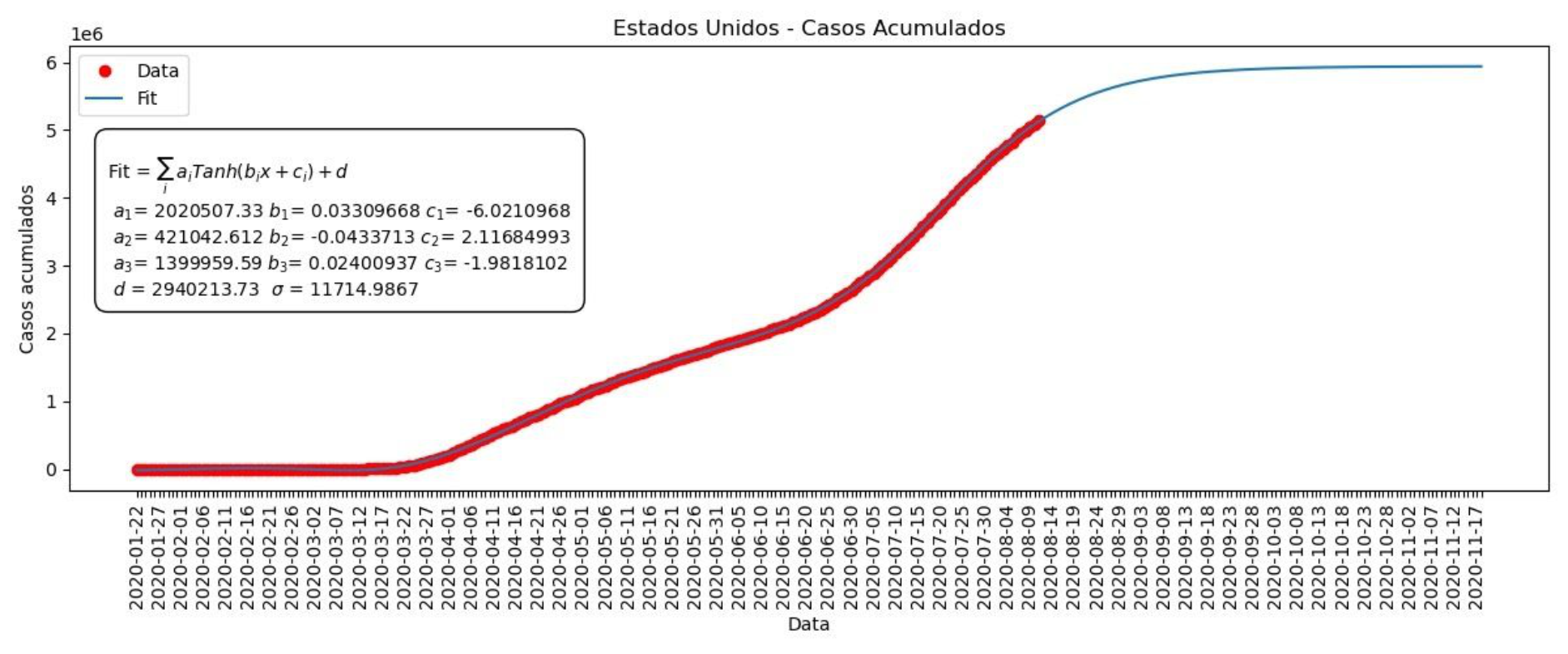
Gráfico 10 – Mortes acumuladas nos Estados Unidos
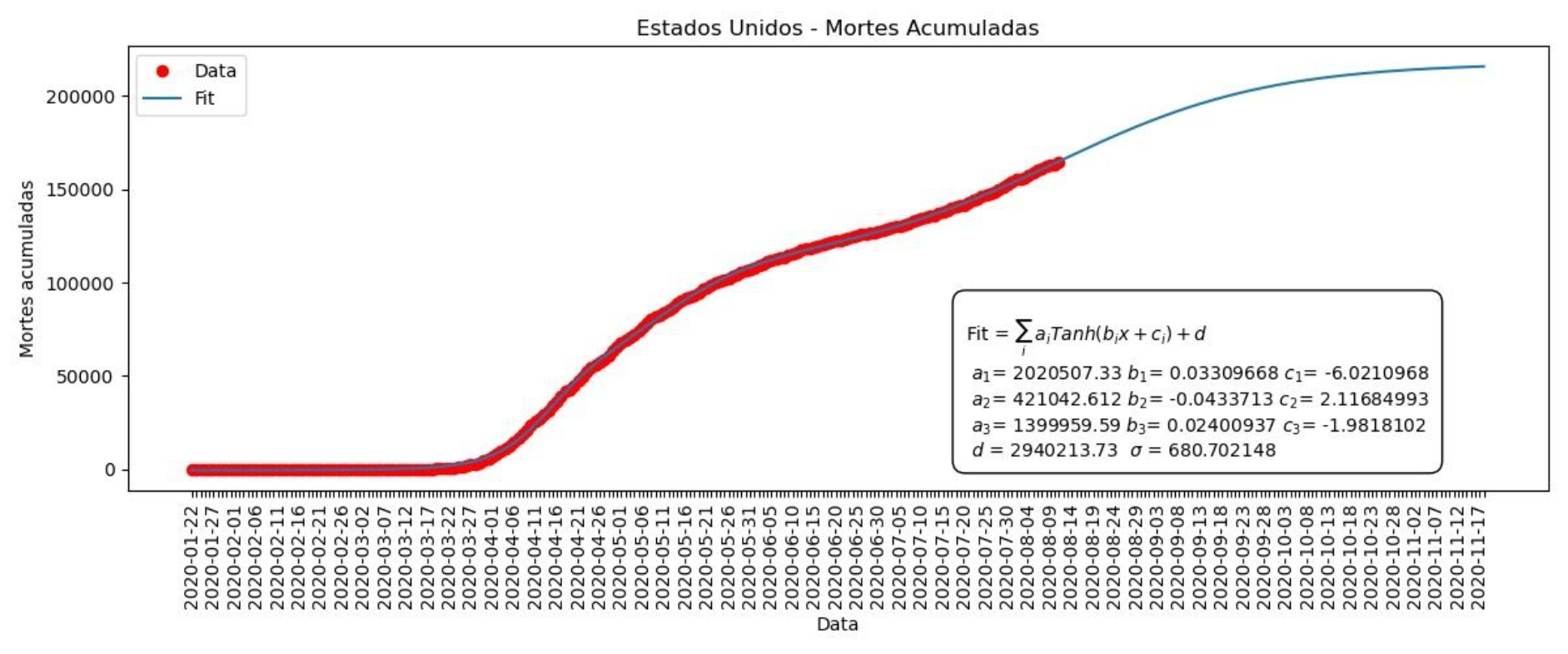
Gráfico 11 – Mortes por dia nos Estados Unidos
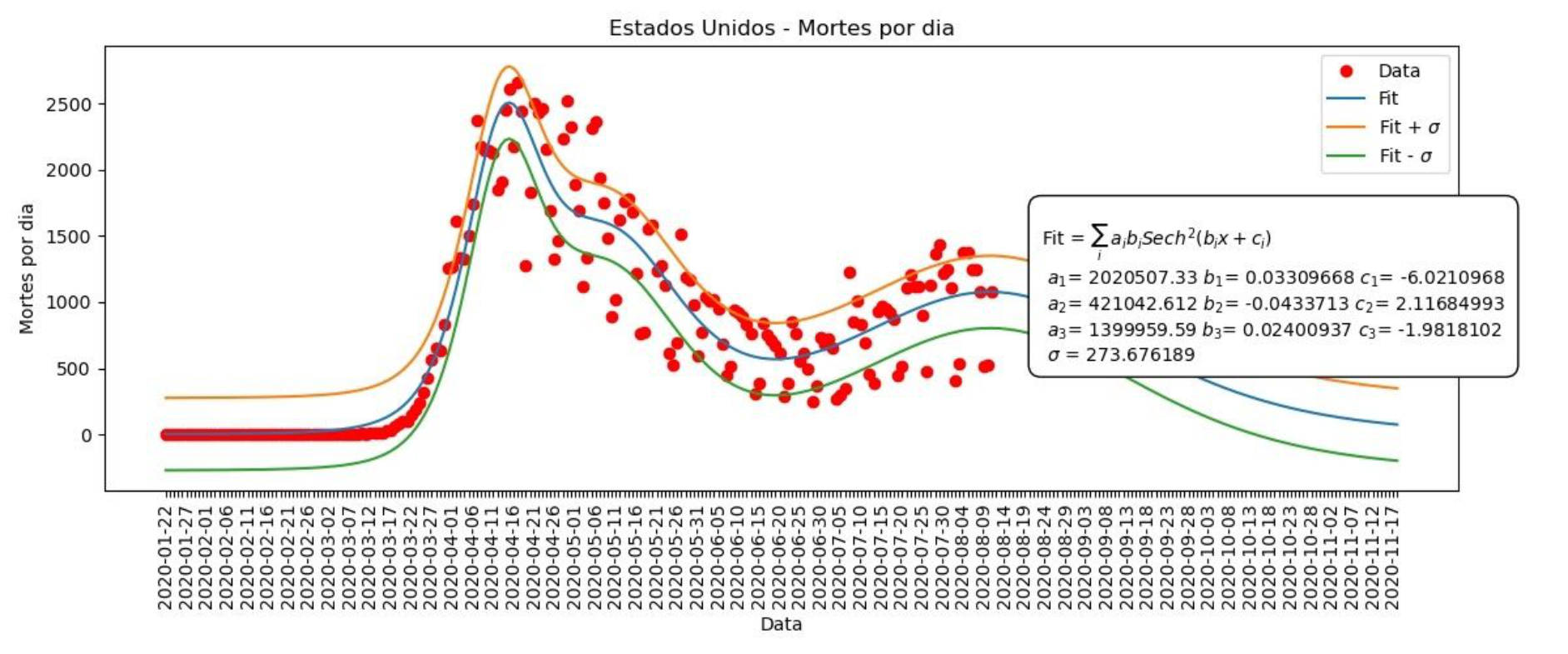
Assim como no caso do Brasil, fizemos o ajuste dos parâmetros a partir dos casos/mortes acumulados. Depois, para obtermos a função para os casos/mortes por dia, utilizamos as derivadas da função para os acumulados mantendo os mesmos valores para os parâmetros a, b, c e d.
Vale lembrar que nosso modelo nos permite fazer previsões assumindo que o comportamento das taxas de contágio e mortes se mantenham as mesmas, dado que apenas consideramos os dados obtidos até então para ajustar nossas funções. Caso surjam novas ondas de contágio e mortes, uma vacina para o COVID-19, ou novas medidas de tratamento e contenção da doença, os ajustes feitos em uma determinada data podem não corresponder aos futuros dados. Neste caso, seria necessário um novo ajuste, levando em conta os dados mais atuais, para que possamos fazer uma nova previsão.
Outra possibilidade é o uso do modelo SEIRD, uma outra versão do modelo SEIR, levando em conta também os recuperados.
Modelagem SEIRD
O modelo compartimentalizado SIR
O modelo SIR
– Suscetíveis, Infectados, Recuperados) é o modelo mais utilizado no mundo para projeção e acompanhamento da pandemia da Covid-19. O modelo foi desenvolvido por William Ogilvy Kermack e A. G. McKendrick em 1927 como uma proposta para determinar os fatores que influenciam na magnitude e tempo de ocorrência de epidemias infecciosas. Os autores trataram a transmissão da doença infecciosa da seguinte forma: Uma ou mais pessoas infectadas são introduzidas em uma comunidade (país, estado, cidade etc) de indivíduos saudáveis e com certa suscetibilidade à doença em questão. A doença se espalha das pessoas infectadas para as suscetíveis através de contato físico. Cada pessoa contaminada passa pelo curso da doença e posteriormente é retirada do número de infectados, passando para o grupo dos removidos (recuperados ou mortos), transição que ocorre segundo as taxas de recuperação e mortalidade. Os autores consideraram que o tempo de ocorrência de uma epidemia é relativamente curto em relação ao tempo de vida de um indivíduo, dessa forma a população total permanece constante ao longo do tempo de ocorrência da doença e o cálculo do número de indivíduos em cada estágio (compartimento) ao longo do tempo pode ser feito através de equações diferenciais não-lineares, a seguir.
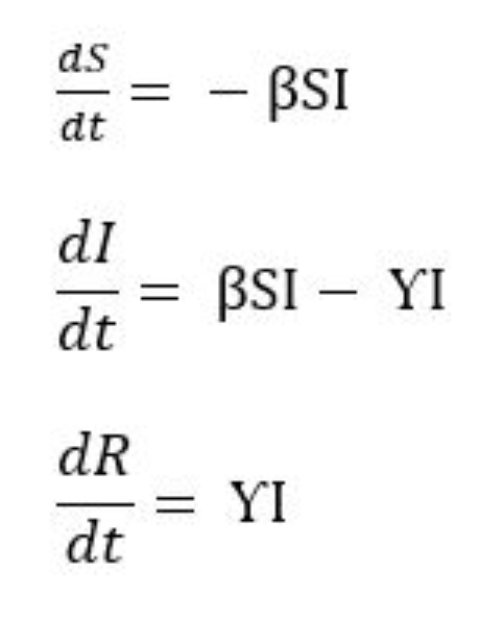
Nestas equações, as variáveis significam:
S: Suscetíveis
I: Infectados
R: Removidos (Recuperados e Mortos)
β: Taxa de infecção
Ƴ: Taxa de remoção
Os termos dS/dt, dI/dt e dR/dt são as taxas de variação de S, I e R com relação ao tempo. Enquanto S, I e R fornecem os números totais de cada quantidade em uma determinada data, dS/dt, dI/dt e dR/dt informam o quanto estas quantidades aumentaram ou diminuíram numa determinada data. Desta forma, por exemplo, a primeira equação nos diz que a variação no número de pessoas suscetíveis é inversamente proporcional a quantidade de pessoas suscetíveis e ao número de infectados e a taxa de infecção da doença.
Modelo compartimentalizado SEIRD
A partir da proposta do modelo SIR diversos outros modelos foram gerados, buscando o aumento da complexidade e capacidade de simulação de um cenário real. O modelo compartimentalizado SEIRD (Susceptible, Exposed, Infectious, Recovered, Death – Suscetíveis, Expostos, Infectados, Recuperados e Mortos) considera mais dois compartimentos nos quais ocorre fluxo de indivíduos no decorrer da epidemia: Expostos (pessoas que foram contaminadas, mas estão em período de incubação da doença) e número de Mortos (através do qual a taxa de mortalidade pode ser avaliada separadamente). O modelo SEIRD também é calculado através de equações diferenciais não-lineares e tem a seguinte estrutura:
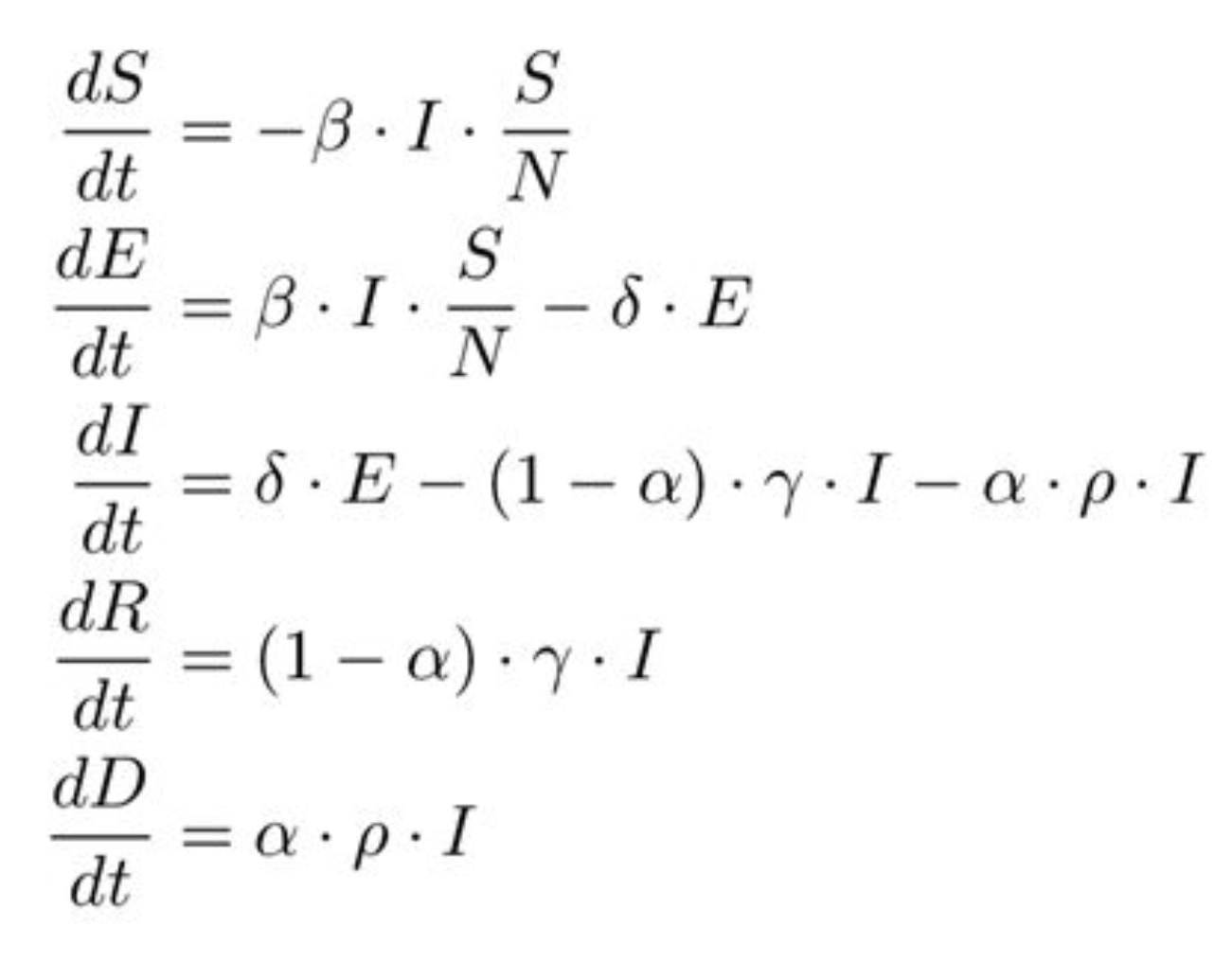
Nesta fórmula, as variáveis significam:
N: População total
S: Suscetíveis
E: Expostos
I: Infectados
R: Recuperados
D: Mortos
β: Infectados por dia por infectado (β = R₀ / D)
D: Dias que a infecção dura
γ: Proporção diária de recuperados (γ = 1/D)
R₀: Total de infectados por infectado (R₀ = β / γ)
δ: Período de incubação
α: Taxa de mortalidade
ρ: Período da infecção até morte
Mais uma vez os termos na forma dX/dt indicam as taxas de variação diárias de cada quantidade. No Gráfico 12, temos um exemplo de como esses valores se comportam.
Gráfico 12 – Modelagem SEIRD
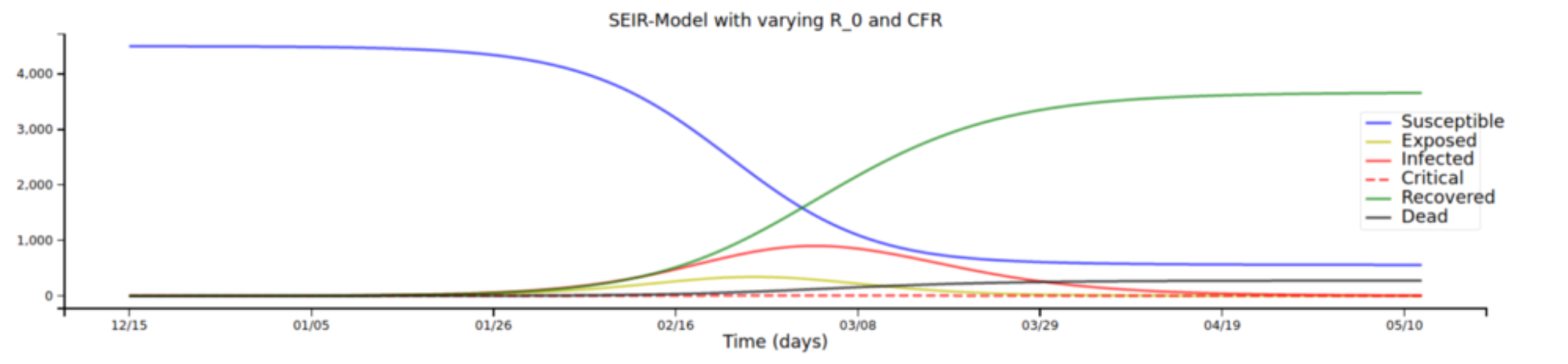
Legenda: Simulação com o modelo SEIRD do ebola adaptado para Covid, alterando as variáveis R_0 (taxa de contágio) e CFR (taxa de letalidade). Na legenda, em ordem: suscetíveis, expostos, infectados, casos críticos, recuperados e mortos. No eixo vertical está a quantidade e, no eixo horizontal, a data. Este modelo em específico leva em conta casos críticos. Fonte: Henri Froese (2020).
O modelo é construído de maneira que a quantidade total de pessoas se mantenha constante (S+E+R+I+D = N), e permita prever o valor de cada uma destas quantidades.
Para realizar previsões com o SEIRD precisamos encontrar valores numéricos para seus parâmetros (𝝰, 𝞫, 𝛄, 𝜹 e 𝝆) tal que as equações do modelo correspondam aos dados que temos para a doença (total de mortes, casos confirmados etc). Contudo, não fomos capazes de encontrar valores que satisfaçam essas condições. Em nossas tentativas sempre obtivemos valores nos quais as previsões do modelo ficaram muito distantes dos dados disponíveis, o que nos impediu de utilizar o modelo para realizar previsões futuras.
Conclusão
O modelo SEIRD baseia-se no tradicional modelo SIR, que é utilizado para a modelagem matemática de diversas epidemias há anos. Dado isso, é possível que utilizemos o SEIRD para modelar a situação brasileira, pois assim poderíamos comparar os ajustes para o nosso caso com os ajustes feitos para outros países, como os Estados Unidos, ou ainda, para os ajustes feitos por outros pesquisadores para o cenário brasileiro. Por outro lado, outros tipos de análise são possíveis, como por meio de nosso modelo de ondas de contágio (OC). Ele utiliza uma nova abordagem, não permitindo uma comparação direta com ajustes e modelos realizados por outros pesquisadores, mas sim trazendo insights para os próximos estudos dessa natureza.
Algumas características dos modelos SEIRD e OC que podemos comparar são:
- O modelo OC tem uma quantidade variável de parâmetros a serem ajustados, sendo três para cada onda de infecção mais um (ai, bi, cie d, onde i é a quantidade de ondas). Enquanto isso o modelo SEIRD sempre tem cinco parâmetros a serem ajustados (𝝰, 𝞫, 𝛄, 𝜹 e 𝝆).
- No modelo OC podemos apenas prever as mortes e os casos acumulados e diários. Já no modelo SEIRD, é possível obter também a quantidade de pessoas suscetíveis, recuperadas e expostas a doença, além de prever a quantidade total de pessoas infectadas em um dado instante, ao invés de prever apenas os valores acumulados.
- Como a quantidade de parâmetros do modelo SEIRD é fixa e eles não variam com o tempo, ele não é capaz de reproduzir um cenário com diversas ondas de infecção. No SEIRD há apenas uma onda, com um único pico de infecções. Já no OC podemos ajustar o modelo para quantas ondas de infecção forem observadas. Entretanto, quanto maior o número de ondas, mais difícil este ajuste.
- Tanto o SEIRD quanto o OC fazem previsões válidas assumindo que seus parâmetros não variem com o tempo. No caso do SEIRD, isso significa que a capacidade de infecção da doença e sua letalidade se mantenham constantes, algo que a princípio pode variar dependendo das condições gerais de saúde da população. Caso estas condições mudem, faz-se necessário encontrar novos valores para os parâmetros. Uma maneira de fazer isso é automatizar a busca por esses parâmetros em um banco de dados atualizado, embora não seja uma tarefa nada fácil. No caso do OC, é necessário que uma vez ajustados os valores dos parâmetros, não surja uma nova onda de contágio. Caso isso ocorra, é necessário refazer os ajustes para o modelo, considerando mais um termo na forma a Tanh(b x + c) para representar a nova onda.
Por fim, uma vez que os dados não se apresentaram suficientes para encontrar valores para os parâmetros do SEIRD que satisfaçam os dados, uma nova abordagem foi elaborada: o modelo OC. Do ponto de vista computacional, os ajustes do modelo OC que realizamos levam poucos minutos e replicam muito bem os dados experimentais disponíveis. Já com o SEIRD, após horas de processamento computacional, não conseguimos resultados satisfatórios. Outro fator favorável ao OC é a capacidade de ajustar casos com diversas ondas de infecção, algo que o SEIRD a princípio não pode fazer. Com isso, considerou-se mais confiável a escolha do modelo OC em vez do SEIRD, dadas as limitações do segundo.
Acerca do uso de Big Data nas modelagens, isso não foi possível nas primeiras epidemias, mas ao longo do tempo isso foi viabilizado, como no caso do monitoramento do Covid. Em epidemiologia, o registro da primeira modelagem é datado de 1760, com o trabalho de Daniel Bernoulli sobre a varíola. Esse e os modelos que vieram depois tiveram como objetivo analisar e modelar o comportamento e a evolução de determinada doença em uma população ao longo do tempo. Eles também permitiram um melhor controle da propagação de doenças, de modo a evitar o avanço de epidemias, assim como prever ações de vacinação e suas consequências. De fato, nenhuma das outras epidemias apresentou um monitoramento tão preciso e eficiente por meio de bancos de dados quanto o Covid, o que tornou possível um estudo analítico baseado em ciência de dados. Este estudo embasou a tomada de decisões tanto por parte do governo, como o controle do isolamento social e de medidas de higiene rigorosas para a população, quanto da população, que pôde tomar seus próprios cuidados. Tudo isso para garantir uma boa qualidade de vida, mesmo em um tempo tumultuado como esse da pandemia.
REFERÊNCIAS
William Ogilvy Kermack and A. G. McKendrick: A contribution to the mathematical theory of epidemics, 1927. (https://royalsocietypublishing.org/doi/10.1098/rspa.1927.0118)
Tibério Borges Vale: Análise da evolução de epidemia COVID-19 em Santo Antônio de Pádua e municípios próximos, 2020. (http://www.professores.uff.br/tiberio/wp-content/uploads/sites/89/2020/05/analise-COVID19-no-Noroeste-Fluminense-v1.0.pdf)
Lucymara de Resende Alvarenga: modelagem de epidemias através de modelos baseados em indivíduos, 2008. (https://repositorio.ufmg.br/bitstream/1843/RHCT-7JXPK4/1/350m.pdf)
Nipun Aggarwal: Importance of Social Distancing: Modeling the spread of 2019-nCoV using Susceptible-Infected-Quarantined-Recovered-t model, 2020. (https://www.medrxiv.org/content/10.1101/2020.04.17.20069245v1.full.pdf)
Henri Froese: Infectious Disease Modelling: Fit Your Model to Coronavirus Data, 2020. (https://towardsdatascience.com/infectious-disease-modelling-fit-your-model-to-coronavirus-data-2568e672dbc7)
REFERÊNCIAS NUMERADAS
- W. Hamer, The Milroy lectures on epidemic disease in England: the evidence of variability and of persistency of type, Bedford Press, 1906.
- Wang, Z., Andrews, M. A., Wu, Z. X., Wang, L., & Bauch, C.T. (2015). Coupled disease–behavior dynamics on complex networks: A review. Physics of Life Reviews. 15:.1-29, December. Disponível em: <https://doi.org/10.1016/j.plrev.2015.07.006> acesso em: 20/05/20.
- Funk, S., Salathé, M., & Jansen V. A. A. (2010). Modelling the influence of human behaviour on the spread of infectious diseases: a review, J. R. Soc. Interface, 7: 1247-1256).
- Agência Brasil. (2020a). Estudo indica eficácia do isolamento social contra o novo coronavírus. [internet]. Disponível em: Acesso em: 01/06/20.
Autores: Ana Carolina, Jéssica Assunção e Rodrigo Araújo e Castro



