O SARS-CoV-2 (Severe acute respiratory syndrome Coronavirus-2) é um vírus da família Coronaviridae [17] e é responsável pela doença denominada COVID-19. Embora outros sintomas extra-pulmonares como conjuntivite, anoosmia (perda do olfato), ageusia (perda precoce do paladar) e sintomas neurológicos estejam presentes, a COVID-19 é principalmente caracterizada por febre, tosse seca, dispnéia, linfopenia e uma significativa taxa de mortalidade, principalmente devido a complicações respiratórias. Uma grande parcela dos pacientes hospitalizados com COVID-19 apresentam comorbidades preexistentes incluindo diabetes, doenças cardiovasculares, doença pulmonar obstrutiva crônica e doenças oncológicas. Os homens parecem apresentar maior suscetibilidade à infecção e uma apresentação mais grave da doença que leva a uma mortalidade mais elevada.
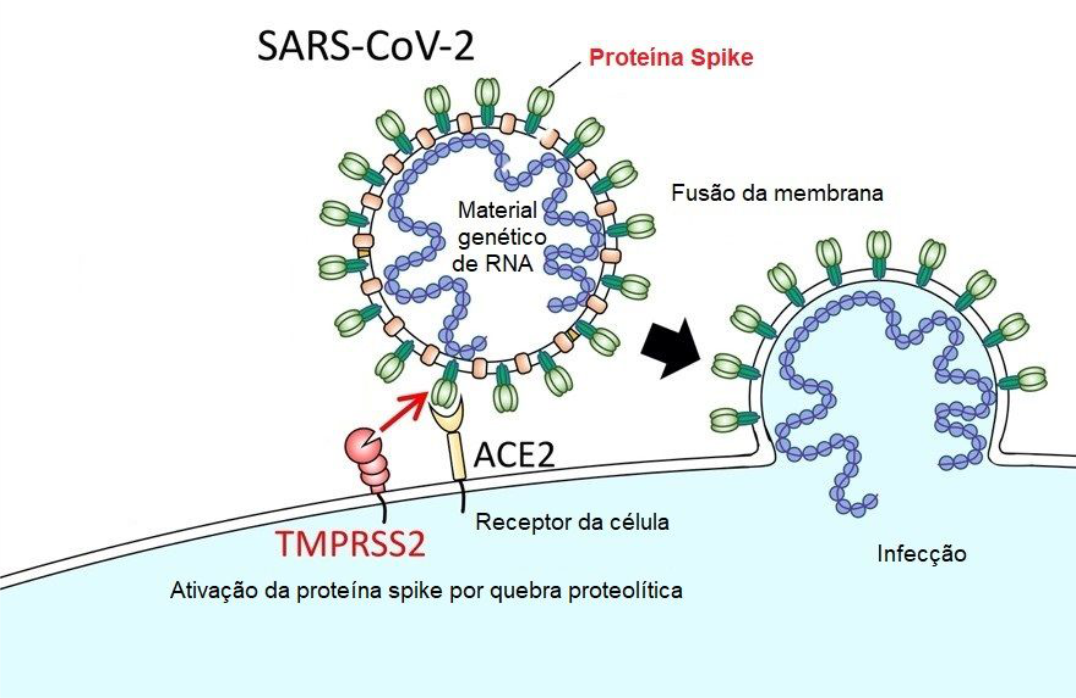
A doença respiratória é a manifestação dominante da infecção pelo SARS-CoV-2, que é adquirida e transmitida pela inalação de gotículas no ar e por vias de contato. A teoria mais aceita é que o SARS-CoV-2 consegue penetrar a célula hospedeira pela interação de uma espícula de proteína do envelope viral com o receptor da enzima conversora de angiotensina-2 (ECA, ACE-2 em inglês) expressa em células epiteliais iniciando a infecção (4, 5, 7, 8, 13, 15–17) (Figura 1).
Figura 1- Infecção da célula epitelial pelo SARS-CoV-2. A espícula protéica na superfície viral é clivada pela enzima TMPRSS2, um tipo especializado de proteína responsável pela ativação de reações moleculares. Após ativada, a espícula viral se liga ao ACE-2, permitindo que o vírus seja fundido à superfície da célula e libere seu material genético, passo inicial para a infecção celular (adaptado de Teodoro Júnior e Carneiro-Ramos, 2020 [15]).
A disseminação da doença se dá sobretudo pelo contato direto entre os indivíduos através de gotículas respiratórias expelidas pela fala, tosse ou espirros, além do contato com superfícies contaminadas. Fica evidente que locais de grande aglomeração de pessoas são focos de disseminação do vírus e incluem farmácias, comércio, escolas e universidades, unidades de saúde e hospitais e também os meios de transporte coletivo. Em grandes centros urbanos mundiais, incluindo São Paulo e outras metrópoles brasileiras, um meio de transporte coletivo com melhor custo-benefício é o metrô, que, assim como outros meios de transporte coletivo são locais propícios para aglomerações, aumentando o rol de locais de propagação do SARS-CoV-2, refletindo uma antiga questão de mobilidade urbana no país e uma preocupação das autoridades na era pós-COVID-19.
O coronavírus possui alta taxa de transmissão. A Organização Mundial da Saúde preconiza um distanciamento mínimo de 1,5m entre os indivíduos. Uma vez que pessoas assintomáticas podem estar transmitindo o vírus, a utilização de equipamentos de proteção bem como medidas higiênicas e de isolamento social, além da redução da exposição a ambientes de aglomeração em geral se tornam medidas de grande relevância no controle da disseminação viral e seriam capazes de reduzir a taxa de infecção pela quebra do ciclo de transmissão do SARS-CoV-2 (Figura 2).
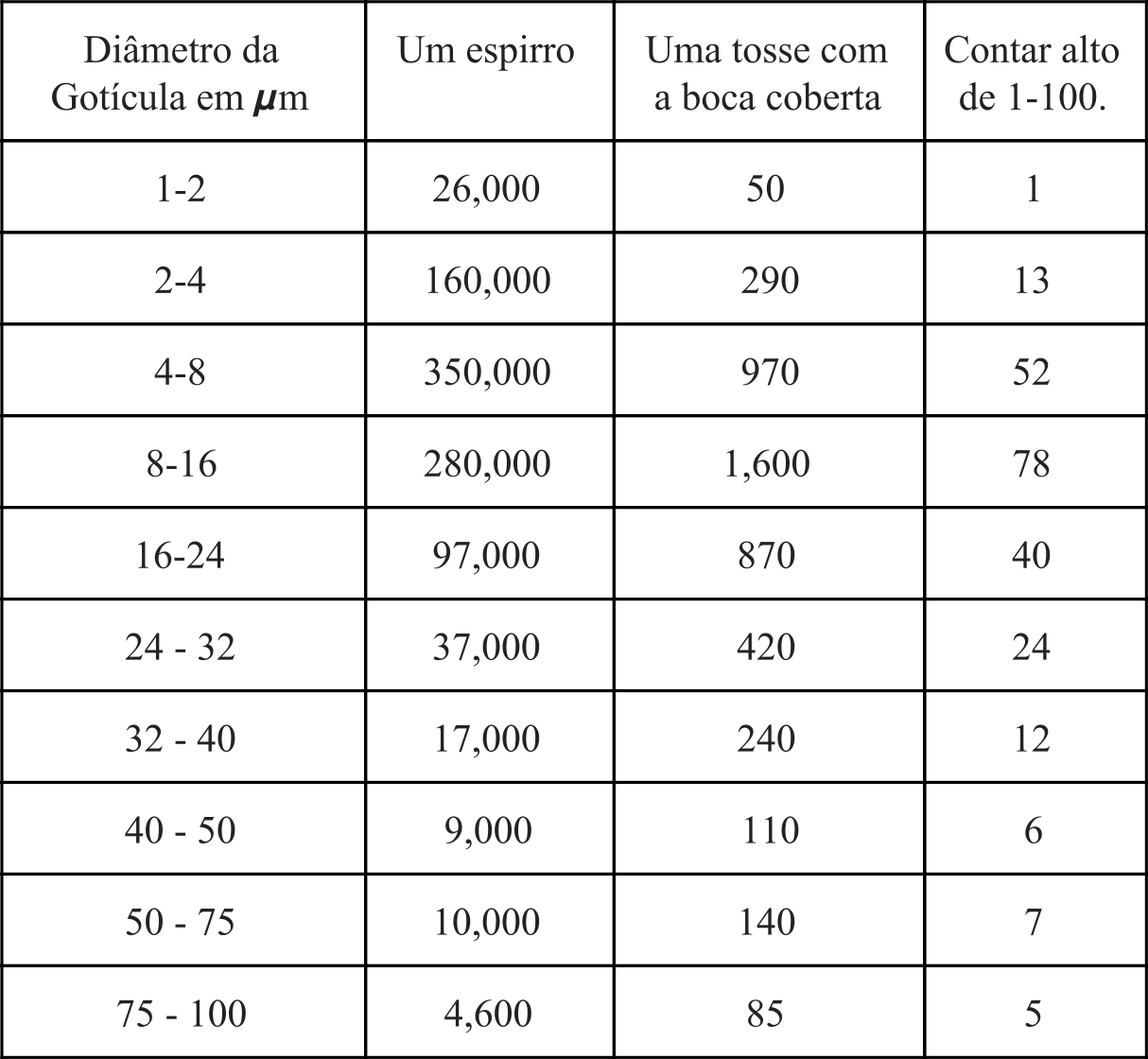
Para que ocorra uma infecção temos que considerar a dose infecciosa do vírus, que para o SARS-CoV-2 ainda não é conhecida, mas acredita-se que uma quantidade de 1 mil a 100 mil cópias do material genético do vírus seja carreada em cada gotícula. Assume-se, deste modo que são necessárias cerca de 1 mil partículas virais para causar a infecção [12]. Entretanto, de acordo com alguns estudos, os aerossóis apresentam um peso menor que o peso de uma gotículas e podem ser transportadas pelo ar a distâncias muito maiores pela corrente de ar. Na tabela 1, temos uma estimativa da quantidade de gotículas liberadas em um espirro, uma tosse ou em uma contagem numérica em voz alta. Com isso, pode-se estimar a quantidade de vírus emitida por um indivíduo, e se compararmos com a quantidade de vírus necessária para causar a infecção, notamos que um indivíduo tem grandes chances de contaminar, ao menos um outro indivíduo.
Tabela 1: Número de gotículas dissipadas em um espirro, uma tosse, e contar até 100 em voz alta (adaptado de Stadnytsky, 2020 [13]).
Com a retomada das atividades econômicas após o fim da quarentena ou o isolamento social com flexibilização horizontal faz-se necessária uma redefinição dos padrões de transporte coletivo. Considerando-se o transporte por meio do metrô, evidencia-se um problema de caráter multifatorial. Nesta estratégia de transporte de pessoas sabe-se que há um expressivo número de indivíduos circulando entre as várias estações; além disso características individuais dos usuários como idade, sexo, presença de comorbidades e condições sociais e abrangência regional do transporte estão, invariavelmente interagindo com características físicas do metrô, quais sejam a ausência ou reduzida quantidade de janelas abertas, espaço confinado com grande número de pessoas, dificuldade ou impossibilidade de higienização das superfícies entre as diversas paradas e a alta rotatividade.
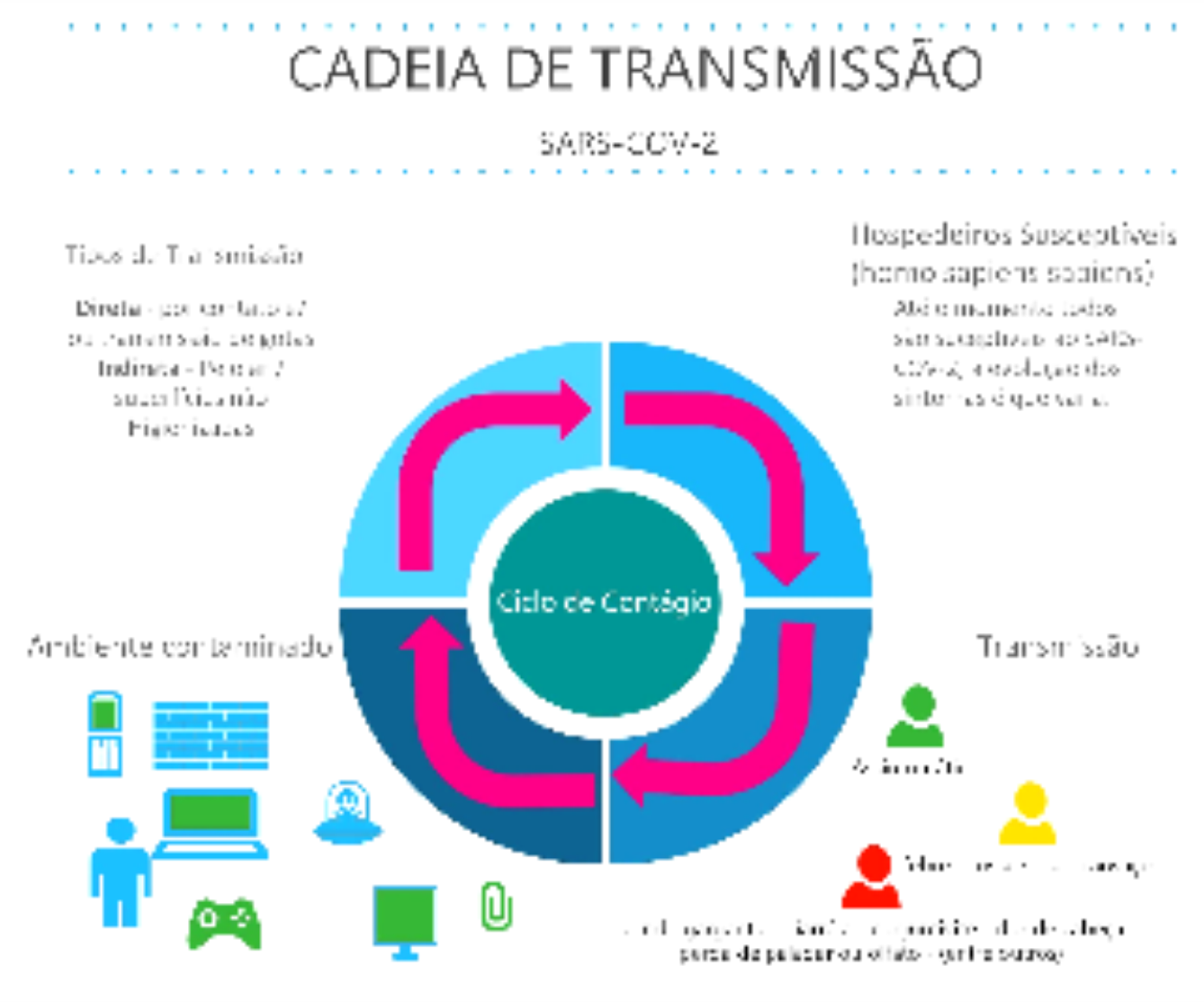
Figura 2: Cadeia de transmissão do vírus SARS-COV-2. Os hospedeiros suscetíveis do SARS-CoV-2 possuem sintomas variáveis que vão desde o assintomático a sintomas graves podendo ser transmitida por pessoas com ou sem sintomas em qualquer fase da infecção. O ambiente de transmissão estão incluídos em um amplo espectro de locais, permitindo a transmissão direta pela inalação de gotículas ou indireta pelo contato com superfícies ou objetos não higienizados. A quebra da cadeia de se dá em quaisquer pontos do ciclo de transmissão.
Empregar o formalismo matemático para expressar relações, previsões, variáveis, parâmetros, entidades e relações entre variáveis e/ou entidades ou operações é o que chamamos de modelagem matemática. Por sua vez, o avanço da interdisciplinaridade possibilitou a aplicação de modelagem matemática à Epidemiologia. Neste contexto, as equações descrevem a interação entre a população e o ambiente, resultando numa análise detalhada a respeito da doença [4,5,6].
Um fator de importância nas análises e modelagens epidemiológicas é determinação da força de infecção, que corresponde à probabilidade de uma pessoa suscetível adquirir a doença [7]. É esta taxa que determina a dimensão da propagação de uma doença infecciosa, assim como o esforço necessário para a sua mitigação [8].
Além disso, a taxa de contágio (Figura 3), que pode ser interpretada como o número de novas infecções determinadas quando um único indivíduo infectado é introduzido em uma população hospedeira suscetível [9]. É esta taxa de contágio que determinará a probabilidade de uma doença se disseminar em uma população. De acordo com o Teorema do Limiar, existe uma densidade mínima de indivíduos suscetíveis, acima da qual é possível o surgimento de uma epidemia transmitida por contato [8]. Portanto, quando TC = 1 tem-se uma situação de equilíbrio e o número de pessoas infectadas na população permanecerá constante. Por outro lado, se TC > 1, o número de casos da doença aumentará e, sendo R0 < 1, o número de infectados vai diminuir até a interrupção do ciclo de transmissão da doença, com o consequente controle do número de indivíduos infectados.
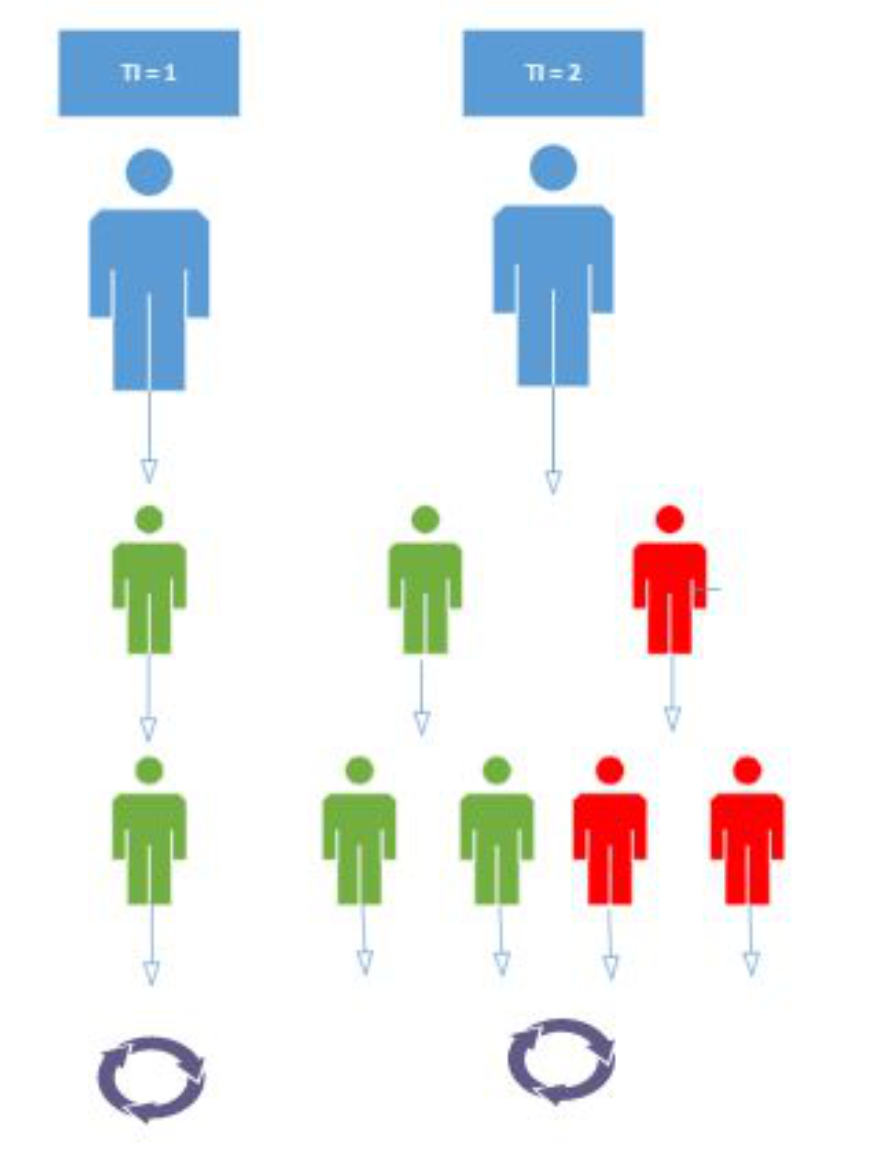
Figura 3: Se TC = 1 (esquerda), uma pessoa infectada infecta uma nova pessoa. Se TC > 1, uma pessoa infectada transmite o vírus a mais de uma pessoa e com isso a doença se espalha cada vez mais. Em azul, temos pessoas suscetíveis, em verde pessoas assintomáticas e em vermelho pessoas com sintomas graves. No fim desse ciclo, ele se repete, contaminando mais pessoas.
Para o Brasil o cálculo da taxa de contágio, baseado em modelagem matemática obtida no aplicativo disponível em public.flourish.studio [10], é dividido por estados, bem como a taxa geral de infecção no país. No presente trabalho, foram utilizadas as taxas de contágio apresentadas no aplicativo do public.flourish.studio [10], para estimar matematicamente a propagação da COVID-19 com a flexibilização da quarentena e a volta do fluxo diário do metrô de São Paulo.
A partir da dinâmica observada na figura 3 pode-se observar que se considerarmos somente o contágio das pessoas sem a influência das demais variáveis, a propagação será representada por uma progressão geométrica, ou seja, a sequência numérica, a partir do segundo termo, é obtida pela multiplicação do termo por uma constante, denominada razão. Resumidamente, se o termo inicial corresponde ao número de indivíduos contaminados usuários do metrô, a razão é igual à taxa de contágio e, do lado direito do sinal, do segundo termo em diante serão os novos contaminados.
número de infectados final =taxa *número de infectados final
Uma outra análise do número de contaminações pode ser realizada considerando-se a curva de contágio como sendo uma curva de crescimento exponencial. Esta curva corresponde a uma função matemática que representa o número de casos em um determinado momento, no caso do novo coronavírus, o número de indivíduos infectados. O crescimento exponencial é caracterizado por um aumento percentual constante em um determinado período de tempo. Na natureza a descrição de um fenômeno por meio do uso de funções exponenciais crescentes é raro, e por sorte, quando ocorrem um tempo limitado, em geral curto, uma vez que os recursos disponíveis são sempre limitados, mesmo que seja a quantidade de humanos. Como as funções exponenciais crescentes têm um crescimento muito acentuado o valor da função rapidamente excede o limite imposto pelos recursos disponíveis.
Método
A taxa de contágio para o Brasil, de acordo estudos do Imperial College of London, varia entre 0.99 e 1.14. Deste modo, em um cenário menos otimista, um único indivíduo irá contaminar uma outra pessoa, tendo aproximadamente 14% de chance de contaminar uma segunda pessoa. No melhor cenário, este indivíduo transmite o vírus a uma única pessoa. No entanto, esta é uma média, uma vez que cada estado do Brasil se encontra em fases distintas da curva de contágio. Exemplificando, enquanto Manaus já passou pelo pico de casos, no estado do Rio de Janeiro os casos continuam crescentes e em São Paulo, estima-se que já se tenha atingido a fase de platô, uma estabilidade. Aqui apresentamos uma estimativa simples de contágio, com a volta progressiva as atividades urbanas e o aumento do fluxo do metrô da cidade de São Paulo.
Considerando-se que a nossa fórmula de cálculo seja para uma progressão geométrica:
infectados(t) =contaminadodia1*taxa de contágio(t -1)
Para o crescimento exponencial, considere-se que a fórmula seja:
infectados (t) = contaminadodia1*etaxa de contágio*t
Sendo:
infectados (t) corresponde ao número de pessoas que o contaminado do dia 1 infectou.
tcorresponde ao número de dias que o contaminado do dia 1 usou o metrô
taxa de contágio é dada para cada estado do Brasil e obtido em public.flourish.studio [10].
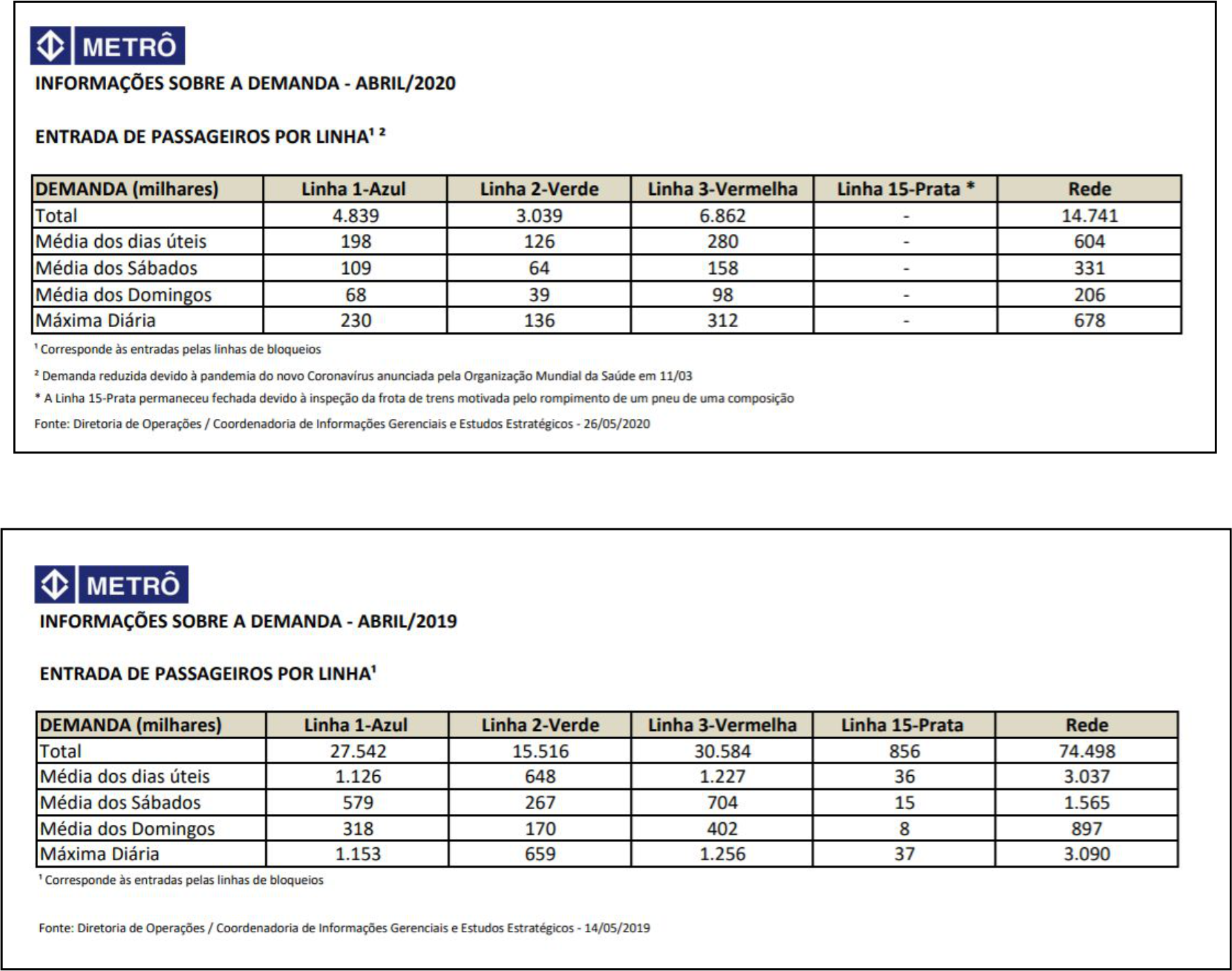
Usando essas duas características de disseminação do SARS-CoV-2 vamos analisar, o contágio no metrô considerando o fluxo de pessoas nos meses de Abril de 2020, período de menor fluxo devido à quarentena, e em abril de 2019. Este é o período em que consideramos que haja o máximo número de de pessoas passando pelo metrô.
É importante considerar que, para esta análise, o único local de contágio é o metrô, e a partir de passageiros contaminados que teriam o potencial de contaminar o local. Ou seja, assumimos que o único evento diário de contágio é a passagem pelo metrô; em uma análise posterior pode ser considerada a propagação ou multiplicação desse contágio. Esta análise não é considerada preditiva, mas sim uma análise estimativa, onde muito provavelmente a ordem de grandeza será atingida. Isto é, não saberemos se serão 200 ou 300 pessoas, mas sim se esse número será da ordem de centenas ou milhares, por exemplo.
Na página do Governo do Estado de São Paulo [12], obtivemos a demanda de abril de 2020, período em que São Paulo estava em regime de quarentena, e comparamos à demanda de abril de 2019, período sem quarentena. Foram realizadas as seguintes considerações:
I – O período de abril de 2019 corresponde a 100% do fluxo do metrô, ou seja, número máximo que este meio de transporte irá atingir após a flexibilização. Ele foi denominado Stotal.
II – O período de abril de 2020 corresponde a uma porcentagem do fluxo total do metrô, que vamos denominar S0.
III – Estimamos uma porcentagem de indivíduos contaminados a partir da quantidade do fluxo de usuários, e variamos o número de passageiros de S0/Stotal até Stotal, portanto, o número de contaminados irá corresponder a:
Stotal*x*y
onde x varia de S0/Stotal até Stotal, e y é estimado, aqui trabalhamos com dois valores 0.3% e 0.5%.
Em nosso estudo, estimamos o contágio de pessoas no metrô de São Paulo, considerando que uma porcentagem dos indivíduos que transitam pelo local esteja contaminada. Para tanto, consideramos os índices de 0.3% e 0.5%. Aqui encontram-se os infectados assintomáticos (indivíduos sem sintomas) que servem de veículo do vírus em uma cadeia de transmissão, os indivíduos com apresentam sintomas gripais, possivelmente com uma maior carga viral (quantidade de vírus em uma amostra de secreção); neste caso, com maior probabilidade de contaminar outras pessoas em um mesmo ambiente.
Resultados
Considerando a taxa de contágio no Brasil, dada pela Imperial College of London, que varia entre 0.99 e 1.14, traçamos as curvas de contágio. Para isso consideramos essas taxas contidas no intervalo q = [0.99, 1.14]. Este intervalo é representado pelas curvas em azul nos gráficos plotados. Portando, a faixa de análise é a faixa entre as curvas, ou seja, a linha vermelha, que representa a taxa média de contágio, isto é, q = 1.065.
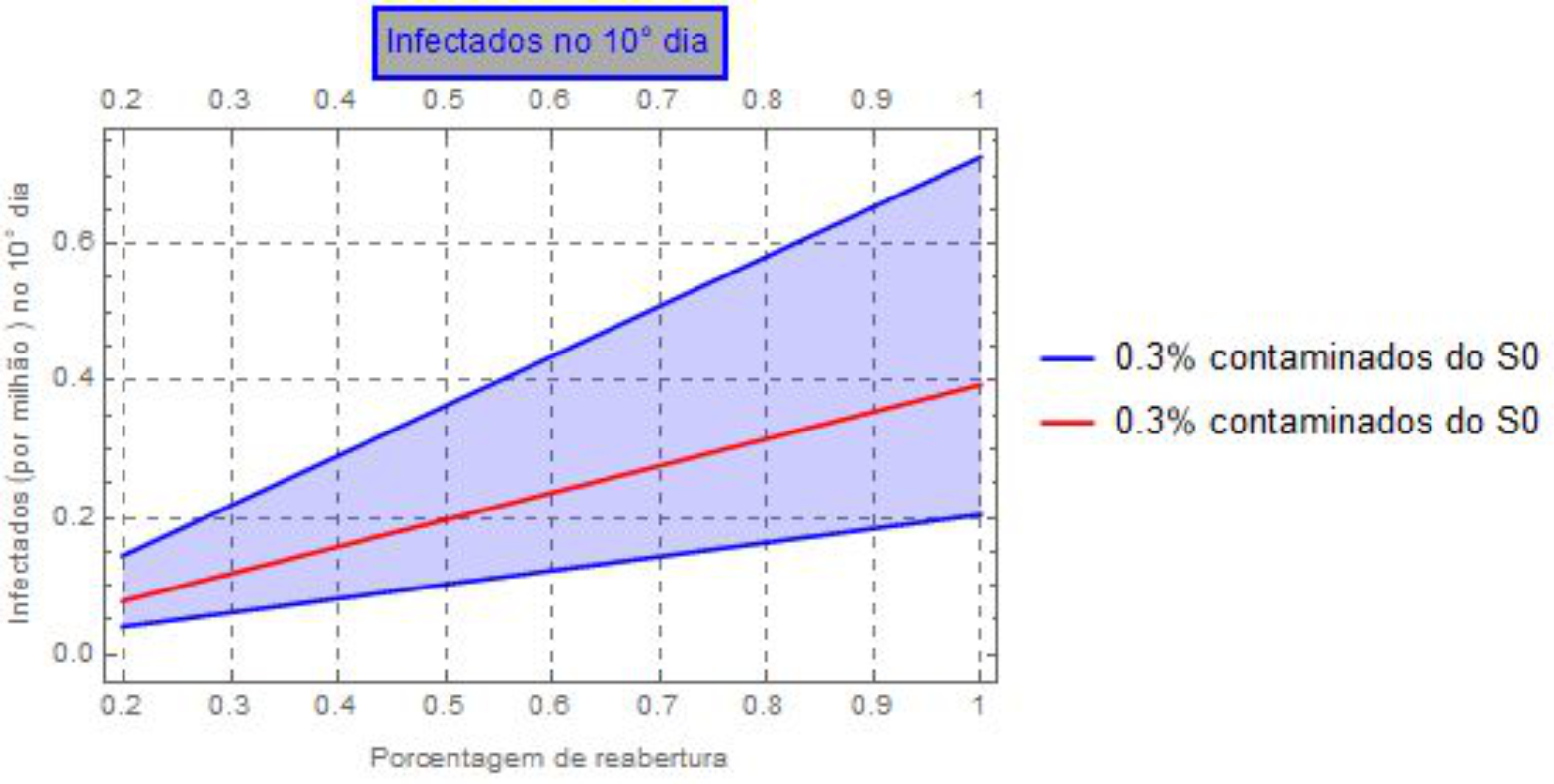
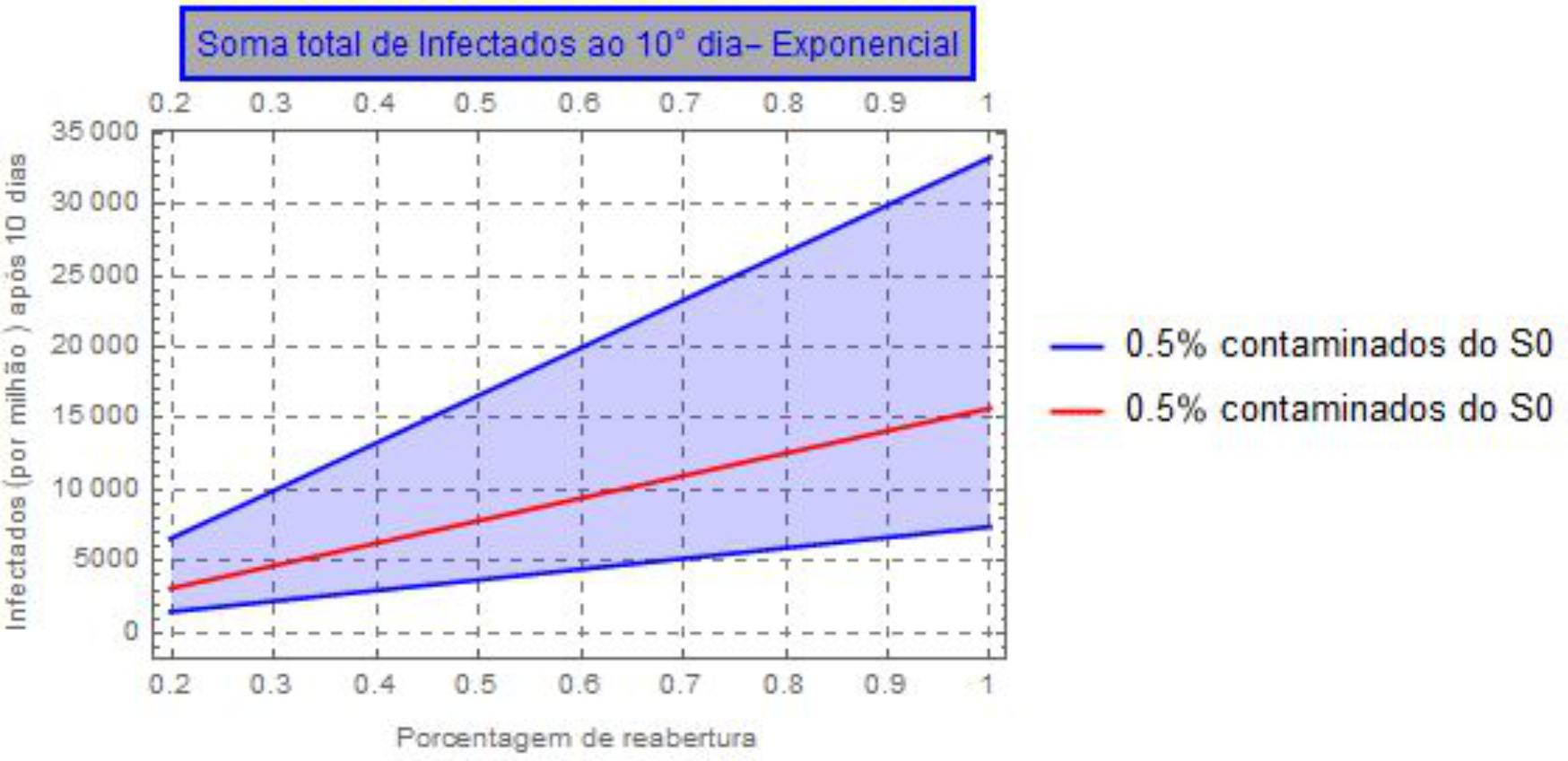
Gráfico 1.1: Estimativa do número de casos no décimo dia de flexibilização, considerando que do total de transeuntes que ingressaram no metrô 0.3% estavam infectados, considerando a curva de contaminação ocorrendo em uma progressão geométrica.
Gráfico 2.1: Número estimado de casos ao décimo dia de flexibilização, considerando que do total de transeuntes que ingressaram no metrô 0.3% estavam infectados, considerando a curva de contágio como sendo uma progressão geométrica.
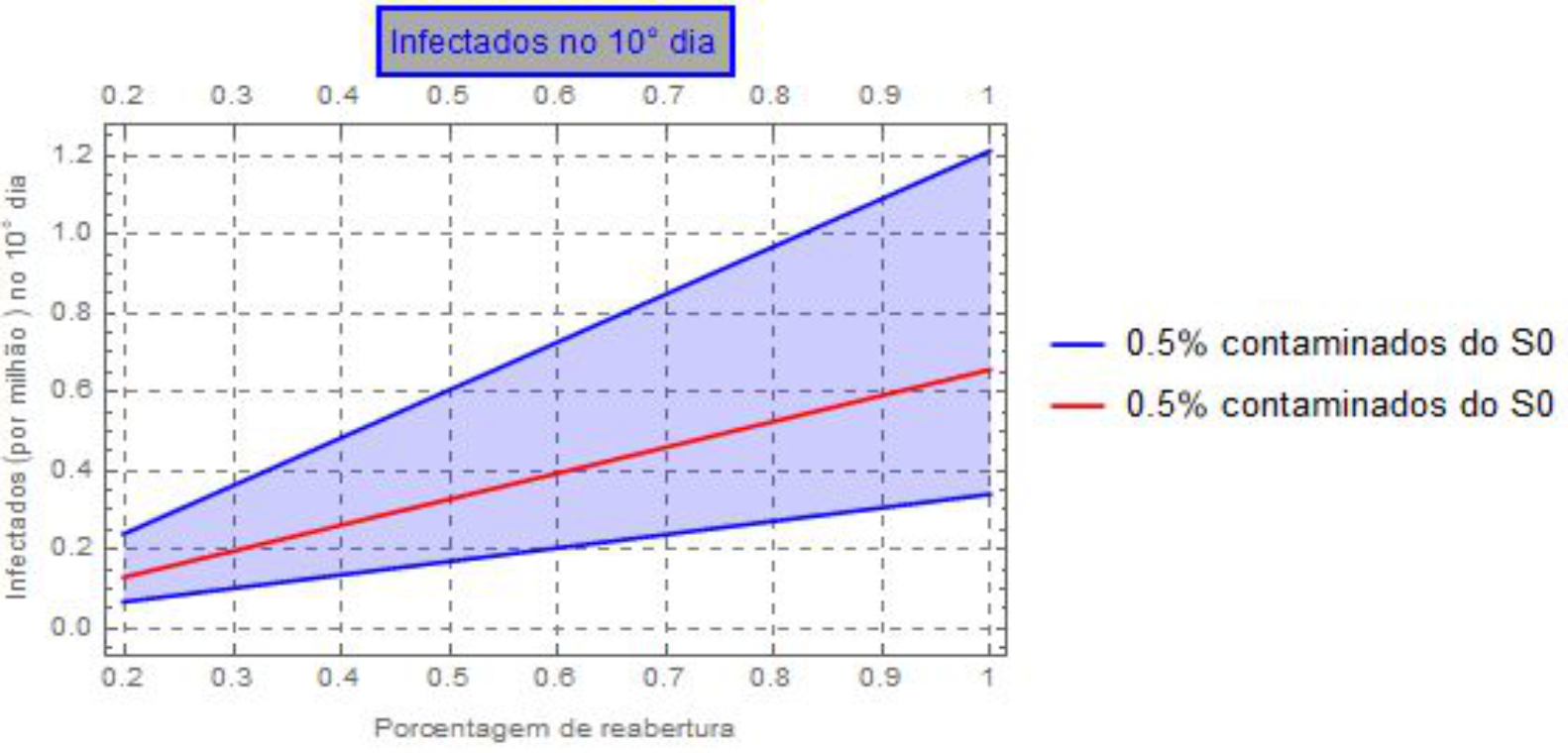
Gráfico 2.2: Número estimado de casos ao décimo dia de flexibilização, considerando que do total de transeuntes que ingressaram no metrô 0.5% estavam infectados, considerando a curva de contágio como sendo uma progressão geométrica.
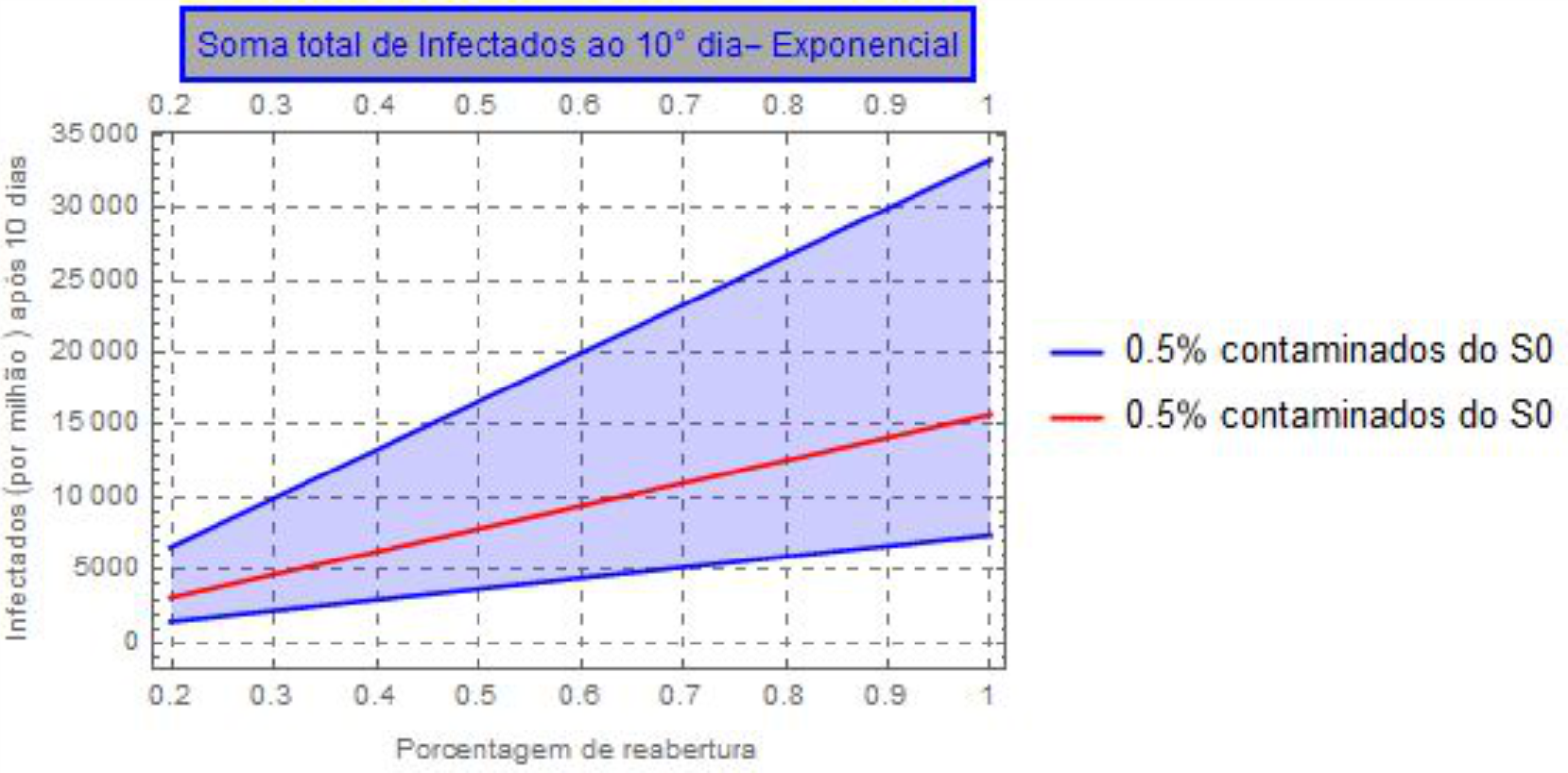
Gráfico 5: Número estimado de casos totais após o décimo dia de flexibilização, considerando que do total de transeuntes que ingressaram no metrô 0.3% estavam infectados, considerando a curva de contágio como sendo uma progressão exponencial.
Gráfico 6: Número estimado de casos totais após o décimo dia de flexibilização, considerando que do total de transeuntes que ingressaram no metrô 0.3% estavam infectados, considerando a curva de contágio como sendo uma progressão exponencial.
As análises representam a estimativa da quantidade de pessoas que seriam contaminadas após dez dias do aumento do fluxo do metrô, por meio da variação do número de usuários. Em abril de 2020 tinha-se aproximadamente 20% menos pessoas utilizando o metrô como meio de transporte em relação à quantidade de usuários em abril de 2019, quando não estávamos em regime de quarentena. Considerando-se que o fluxo de abril de 2019 é o maior fluxo que pode ser atingido, variamos a curva de 20% (abril de 2020) até 100% (abril de 2019) e estimamos quantas pessoas seriam contaminadas na hipótese de reabertura da economia. Isso é uma estimativa, mas a partir dela pode-se estimar por exemplo, a quantidade de pessoas com probabilidade de ocupar leitos hospitalares. Pode-se estimar, ainda, a quantidade de pessoas que podem ser infectadas em casa, tendo em vista o número de indivíduos agindo como veículo de transmissão do vírus suas residências.
Considerações Finais
As análises e os resultados aqui apresentados foram desenvolvidos de acordo com as referências bibliográficas para cálculo de estimativas relacionadas ao contágio do SARS-CoV-2. Uma vez que este é um vírus novo, sobre o qual o mundo ainda está aprendendo e estudando junto às consequência da doença que ele causa, suas características são são bastante peculiares. A partir dessas estimativas, pode-se calcular a quantidade de pessoas com probabilidade de ocupar leitos hospitalares e a quantidade de pessoas que podem ser infectadas em casa, visto que os indivíduos estão agindo como veículo de transmissão do vírus para suas residências.
Para lidar com esse desafio, contamos com a disponibilidade de dados globais em tempo real. Portanto, não precisamos nos limitar a de usar apenas uma modelagem simples de dados, podendo partir para a próxima etapa da análise de dados, o Big Data, exploração de grandes volumes de informação provenientes de redes sociais ou dados disponibilizados digitalmente por órgãos públicos para obter conclusões que não seriam obtidas de outras formas. Com isso, pode-se auxiliar ainda mais a medicina no estabelecimento de estabelecer padrões de comportamento da sociedade para antecipar os próximos “passos” da COVID-19, auxiliando na tomada de decisões.
Bibliografia
1. SILVEIRA, M.R., COCCO R.G. Transporte público, mobilidade e planejamento urbano: contradições essenciais. Estudos Avançados, São Paulo, v. 27, n. 79, p. 41-53, 2013.
2. Rede de transportes sobre trilhos avançou só 10,4 km no Brasil em 2015.
3. DEVAUX A.C., ROLAIN Jean-Marc, RAOULT R, PMID: 32414646,PMCID: PMC7201239, DOI: 10.1016/j.jmii.2020.04.015 J Microb. Immunol. Infec. Volume 53, Issue 3, June 2020, Pages 425-435.
4. LEON C.V. On the global stability of sis, sir and sirs epidemic models with standard incidence. Chaos Sol. Frac., Elsevier ltda, v. 44, p. 1106–1110, 2011.
5. WAKE G.C., KOROBEINIKOV A. Lyapunov functions and global stability for sir, sirs and sis epidemiological models. Appl. Math. Lett. Elsevier, v. 15, p. 955–960, 2002.
6. CAPASSO V. Mathematical Structures of Epidemic Systems. Berlim: SpringerVerlag, 1993.
7. AMAKU M. Estudos de parâmetros epidemiológicos através de modelamento matemático: aspectos estacionários, espaciais e temporais. Tese (Doutorado em ciências). Universidade de São Paulo, USP, São Paulo, 2001;
8. ALVARENGA L.R. Modelagem de epidemias através de modelos baseados em indivíduos. 2008. Tese (Mestrado em Engenharia Elétrica). Universidade Federal de Minas Gerais, UFMG, Belo Horizonte, 2008.
9. ANDERSON R.M, eMAY R.M. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxf. Univ. Press. 1992.
10. https://public.flourish.studio/visualisation/2882061/?utm_source=showcase&utm_campaign=visualisation/2882061
11. http://www.governoaberto.sp.gov.br/relatorios-estatisticos/,
12. ARONS M.M., HATFIELD K.M., REDDY S.C. et al., Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N. Engl. J. Med., April 24, 2020. [cited 2020 Apr 27]. Available from: DOI: https://doi.org/10.1056/NEJMoa2008457.
13. STADNYTSKY, V. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. Proc. Nat. Acad. Sci., v. 117, n. 22, p. 11875-11877, 2020.
14. Duguid JP. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. J. Hyg. (Lond). 1946; 44(6):471-479. doi:10.1017/s0022172400019288.
15. TEODORO JÚNIOR L., CARNEIRO-RAMOS M.S. Como detectar o Novo Coronavírus. Disponível em: https://proec.ufabc.edu.br/epufabc/como-detectar-o-novo-coronavirus/#content (UFABC). Acesso em 16.07.2020, 22h25.
16. COVID-19 [recurso eletrônico] : perguntas e respostas Centro de Telemedicina da UCS / org. Lessandra Michelin, Rodrigo Schrage Lins, Asdrubal Falavigna. – Caxias do Sul, RS: Educs, 2020. Dados eletrônicos. ISBN 978-65-5108-008-1. Modo de acesso: World Wide Web.
17. International Committee on Taxonomy of Viruses (ICTV). In: https://talk.ictvonline.org/taxonomy/.
Autores: Ana Carolina, Jéssica Assunção e Rodrigo Araújo e Castro